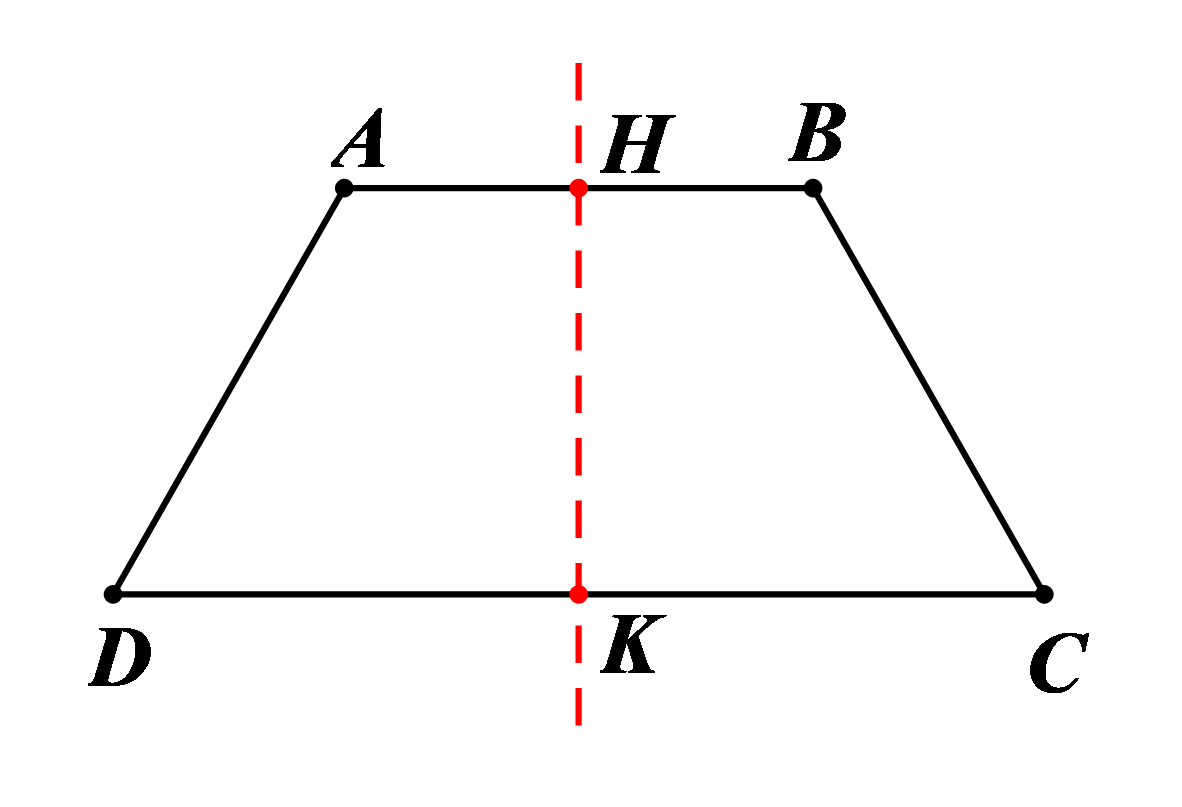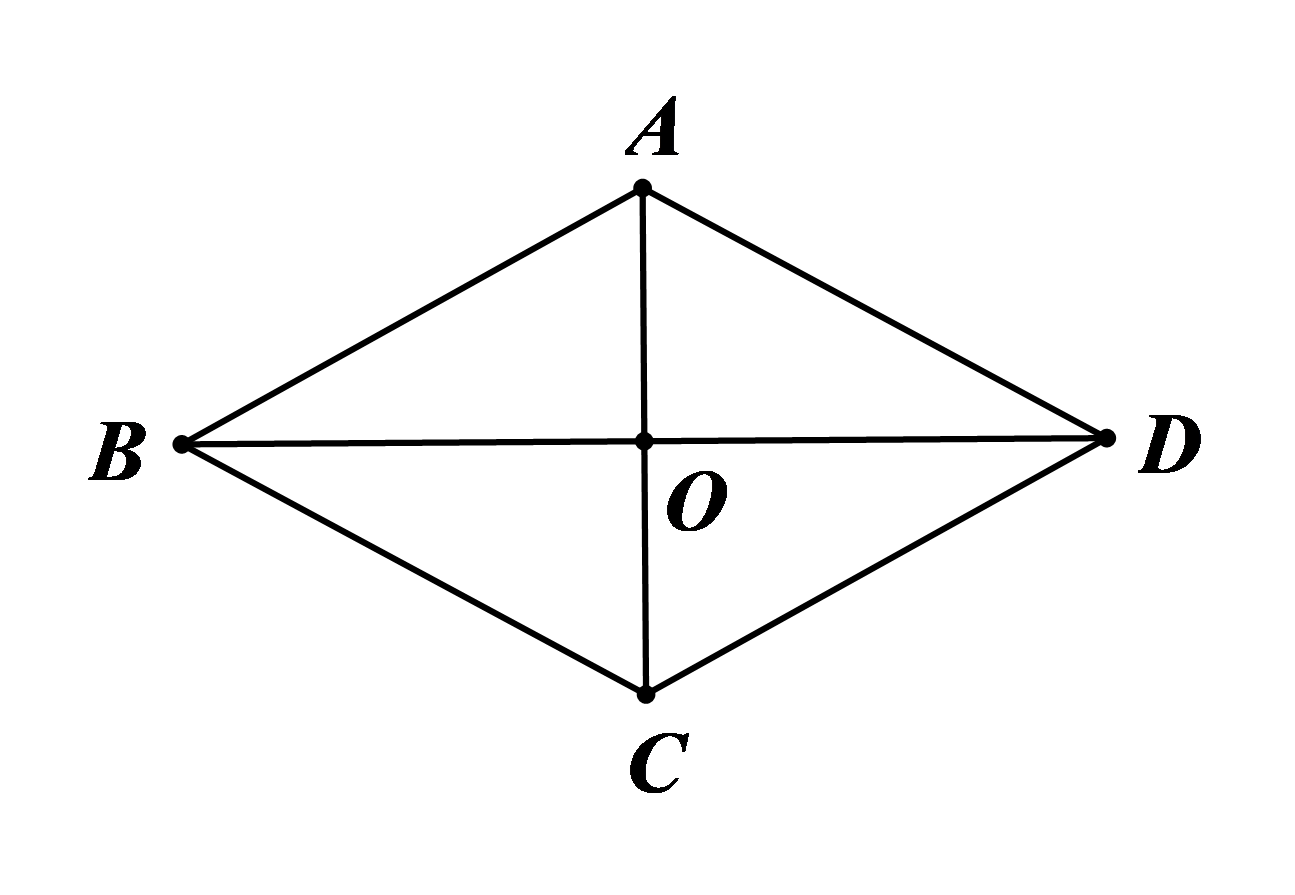Câu hỏi:

24/10/2025 296

Cho các hình sau đây:

(1) Đoạn thẳng $AB;$

(2) Tam giác đều $ABC;$

(3) Hình tròn tâm $O;$

(4) Hình thang cân $ABCD$ (có đáy lớn $CD);$

(5) Hình thoi $ABCD.$

Trong các hình nói trên:

a) Hình nào có trục đối xứng? Chỉ ra trục đối xứng của hình đó.

b) Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó.

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập cuối kì 1 Toán 6 Kết nối tri thức cấu trúc mới có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

a) Cả 5 hình đã cho đều có trục đối xứng như sau:

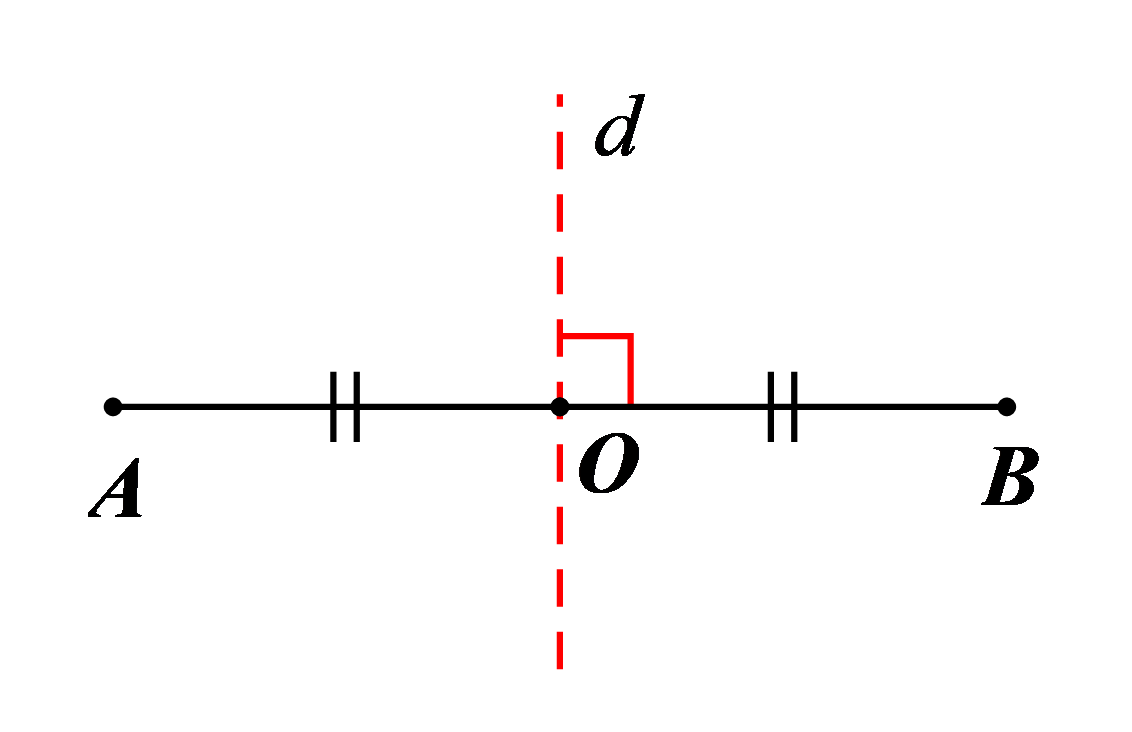
(1) Đoạn thẳng $AB$ là hình có 1 trục đối xứng và trục đối xứng là đường thẳng \[d\] đi qua trung điểm $O$ của đoạn thẳng $AB$ và vuông góc với $AB$ (hình vẽ).	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 1)$
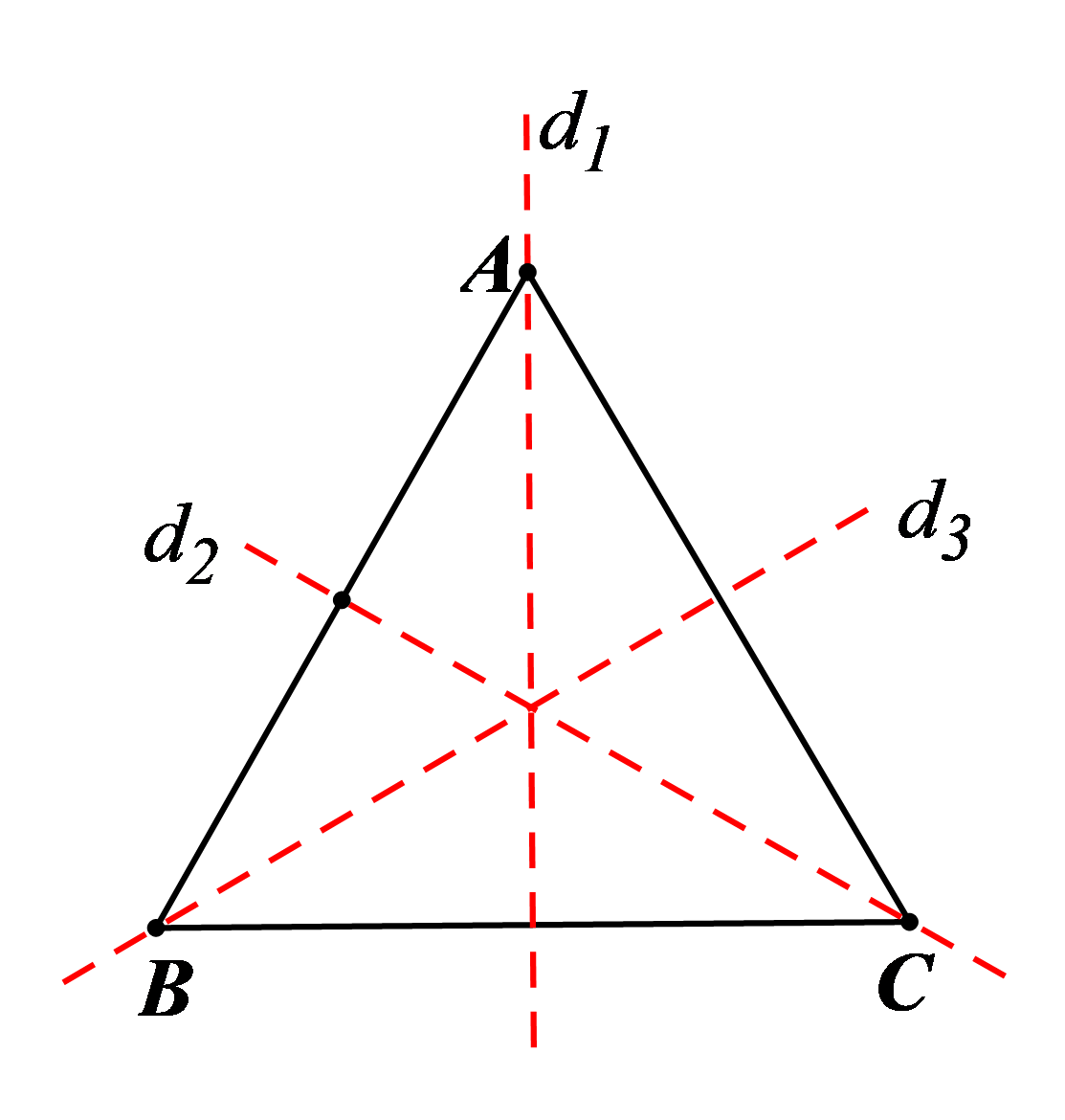
(2) Tam giác đều \[ABC\] là hình có trục đối xứng và có 3 trục đối xứng \[{d_1},{\rm{ }}{d_2},{\rm{ }}{d_3}\;\](hình vẽ).	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 2)$
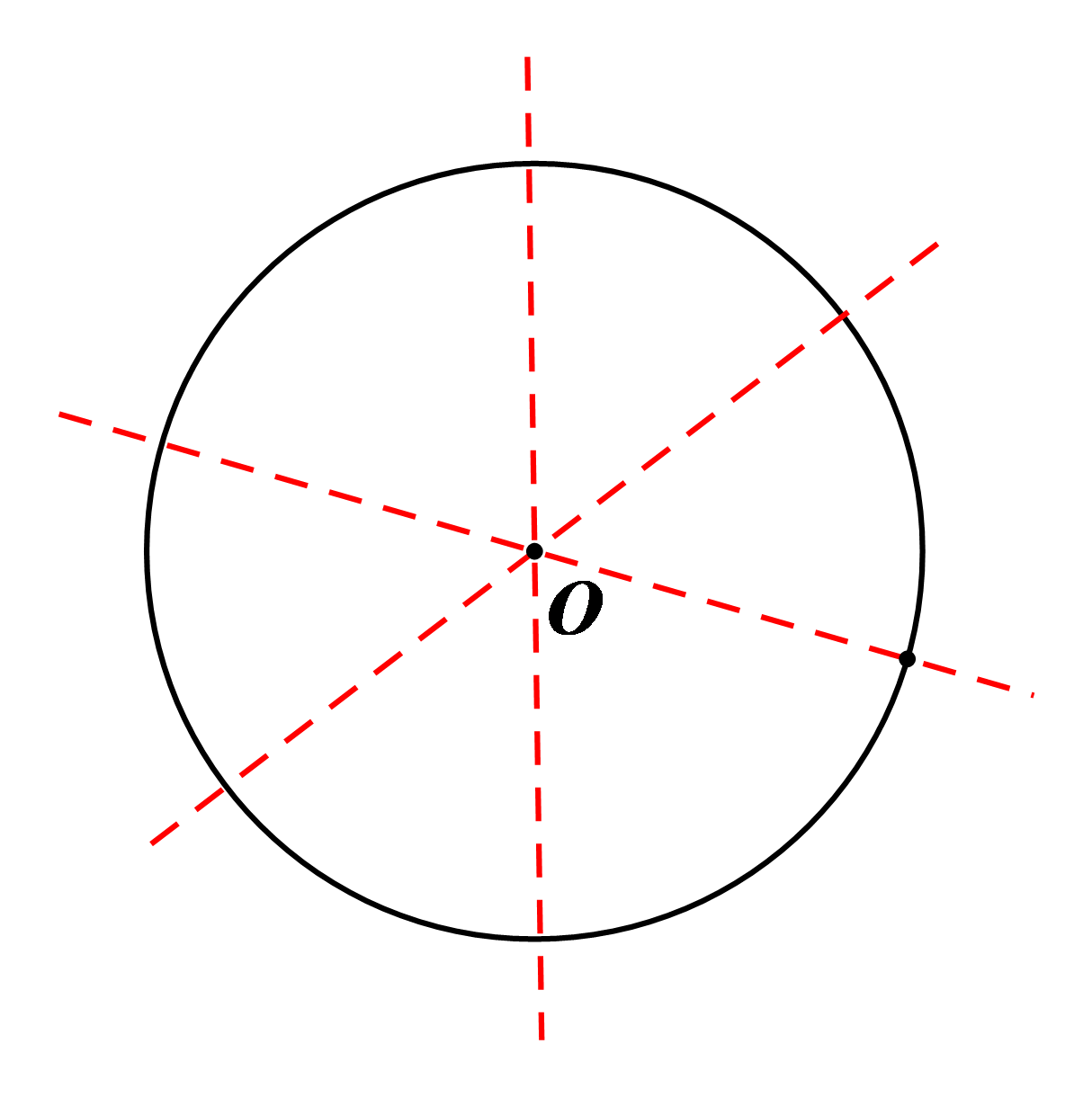
(3) Hình tròn tâm \[O\] có vô số trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm \[O\] của nó.	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 3)$
(4) Hình thang cân \[ABCD\] (có đáy lớn \[CD)\] là hình có 1 trục đối xứng và trục đối xứng là đường thẳng đi qua trung điểm \[H\] và \[K\] của 2 đáy \[AB\] và $CD.$	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 4)$
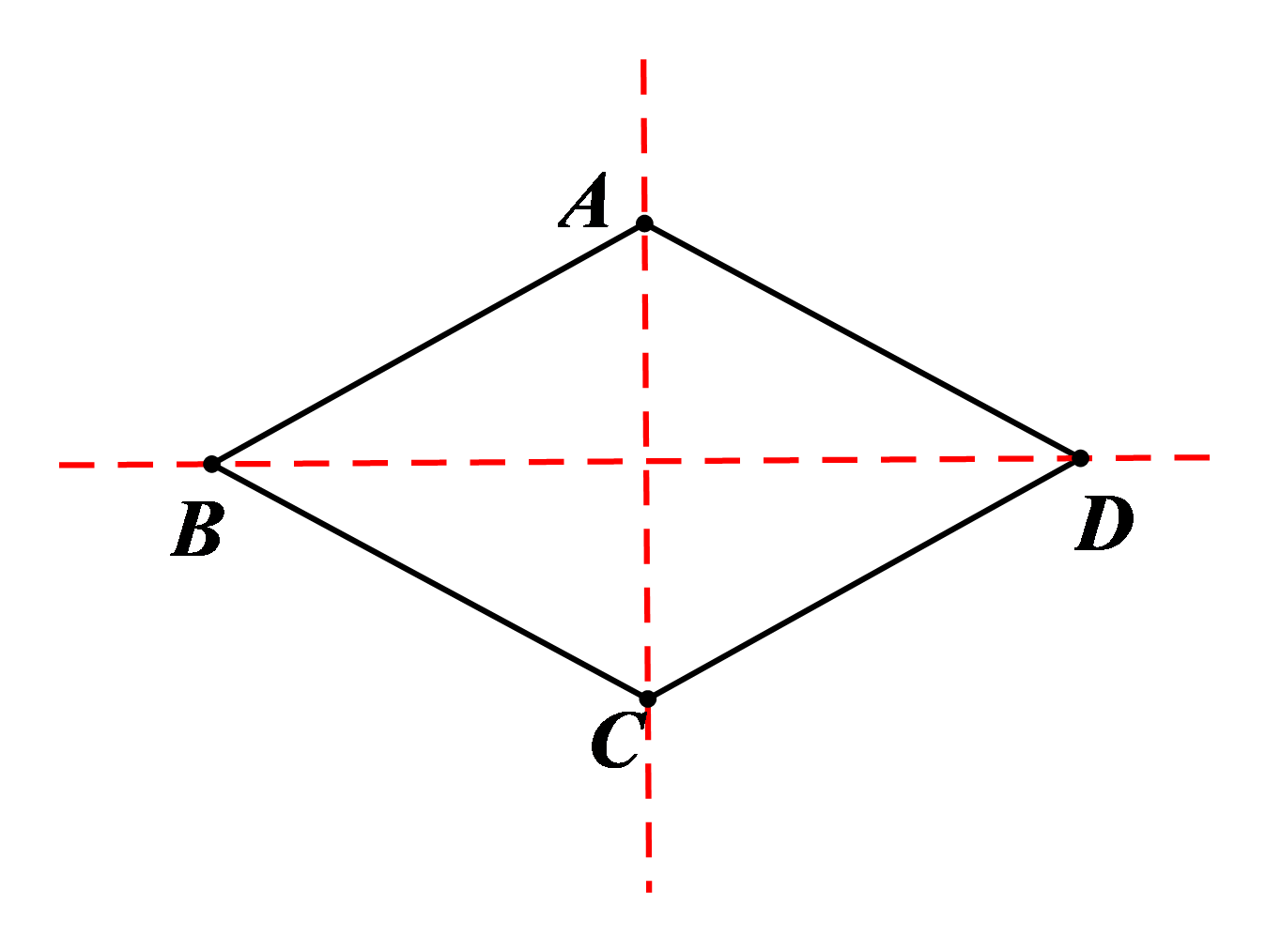
(5) Hình thoi \[ABCD\] có 2 trục đối xứng là hai đường chéo \[AC\] và \[BD.\]	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 5)$

b) Trong 5 hình đã cho: đoạn thẳng \[AB,\] hình tròn tâm \[O,\] hình thoi \[ABCD\] là các hình có tâm đối xứng. Các hình tam giác đều \[ABC,\] hình thang cân $ABCD$ là hình không có tâm đối xứng.

(1) Đoạn thẳng \[AB\] là hình có tâm đối xứng và tâm đối xứng là trung điểm \[O\] của $AB.$	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 6)$
(3) Hình tròn tâm \[O\] có tâm đối xứng chính là tâm \[O.\]	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 7)$
(5) Hình thoi \[ABCD\] có tâm đối xứng là giao điểm \[O\] của hai đường chéo \[AC\] và \[BD.\]	$Cho các hình sau đây: (1) Đoạn thẳng $AB;$ (ảnh 8)$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một thư viện có một số quyển sách cần lưu trữ. Nếu xếp thành bó 10 quyển thì thừa 2 quyển, xếp thành bó 12 quyển thì thừa 4 quyển, xếp thành bó 15 quyển thì thừa 7 quyển. Tính số sách mà thư viện đó cần lưu trữ biết rằng số sách trong khoảng từ 100 đến 150.

Xem đáp án

Lời giải

Hướng dẫn giải

Gọi $x$ (quyển) là số sách mà thư viện cần lưu trữ $\left( {x \in \mathbb{N}*,\,\,100 \le x \le 150} \right)$.

Nếu xếp thành bó 10 quyển thì thừa 2 quyển nên ta có \[\left( {x - 2} \right)\,\, \vdots \,\,10\] suy ra \[\left( {x - 2 + 10} \right)\,\, \vdots \,\,10\] hay \[\left( {x + 8} \right)\,\, \vdots \,\,10\].

Nếu xếp thành bó 12 quyển thì thừa 4 quyển nên ta có $\left( {x - 4} \right)\,\, \vdots \,\,12$ suy ra \[\left( {x - 4 + 12} \right)\,\, \vdots \,\,12\] hay \[\left( {x + 8} \right)\,\, \vdots \,\,12\].

Nếu xếp thành bó 15 quyển thì thừa 7 quyển nên ta có $\left( {x - 7} \right)\,\, \vdots \,\,15$ suy ra \[\left( {x - 7 + 15} \right)\,\, \vdots \,\,15\] hay \[\left( {x + 8} \right)\,\, \vdots \,\,15\].

Do đó \[\left( {x + 8} \right) \in \]BC$\left( {10,\,\,12,\,\,15} \right)$.

Ta có: $10 = 2 \cdot 5;\,\,\,\,\,12 = {2^2} \cdot 3;\,\,\,\,\,15 = 3 \cdot 5.$

Suy ra BCNN$\left( {10,\,\,12,\,\,15} \right) = {2^2} \cdot 3 \cdot 5 = 60$.

Nên BC$\left( {10,\,\,12,\,\,15} \right) = $B\[\left( {60} \right) = \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,...} \right\}\]

Hay \[\left( {x + 8} \right) \in \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,...} \right\}\]

Khi đó \[x \in \left\{ { - 8;\,\,52;\,\,112;\,\,172;\,\,232;\,\,292;\,\,...} \right\}\]

Mà $100 \le x \le 150$ nên $x = 112.$

Vậy thư viện có 112 quyển sách cần lưu trữ.

Câu 2

Một hộp giấy đựng bỏng ngô gồm bốn mặt bên xung quanh và một mặt đáy. Biết mỗi mặt xung quanh của một hộp giấy đó có dạng là một hình thang cân có độ dài các cạnh đáy lần lượt là $13{\rm{\;cm}}$ và $10{\rm{\;cm}}$, chiều cao là $20{\rm{\;cm,}}$ đáy hộp có dạng hình vuông cạnh là $10{\rm{\;cm}}$.

a) Tính diện tích một mặt bên của hộp giấy.

b) Hỏi cần ít nhất bao nhiêu cen-ti-mét vuông giấy bìa để làm một chiếc hộp đựng bỏng ngô đó (không tính diện tích các mép dán)?

Xem đáp án

Lời giải

Hướng dẫn giải

a) Diện tích một mặt của hộp giấy là: \[\frac{{\left( {10 + 13} \right) \cdot 20}}{2} = 230{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]

b) Diện tích bốn mặt xung quanh của chiếc hộp là: $230 \cdot 4 = 920{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}$

Đáy hộp đựng bỏng ngô là hình vuông nên có diện tích là: ${10^2} = 100{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}$

Diện tích giấy bìa ít nhất để làm được một chiếc hộp là: $920 + 100 = 1\,\,020{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}$

Câu 3