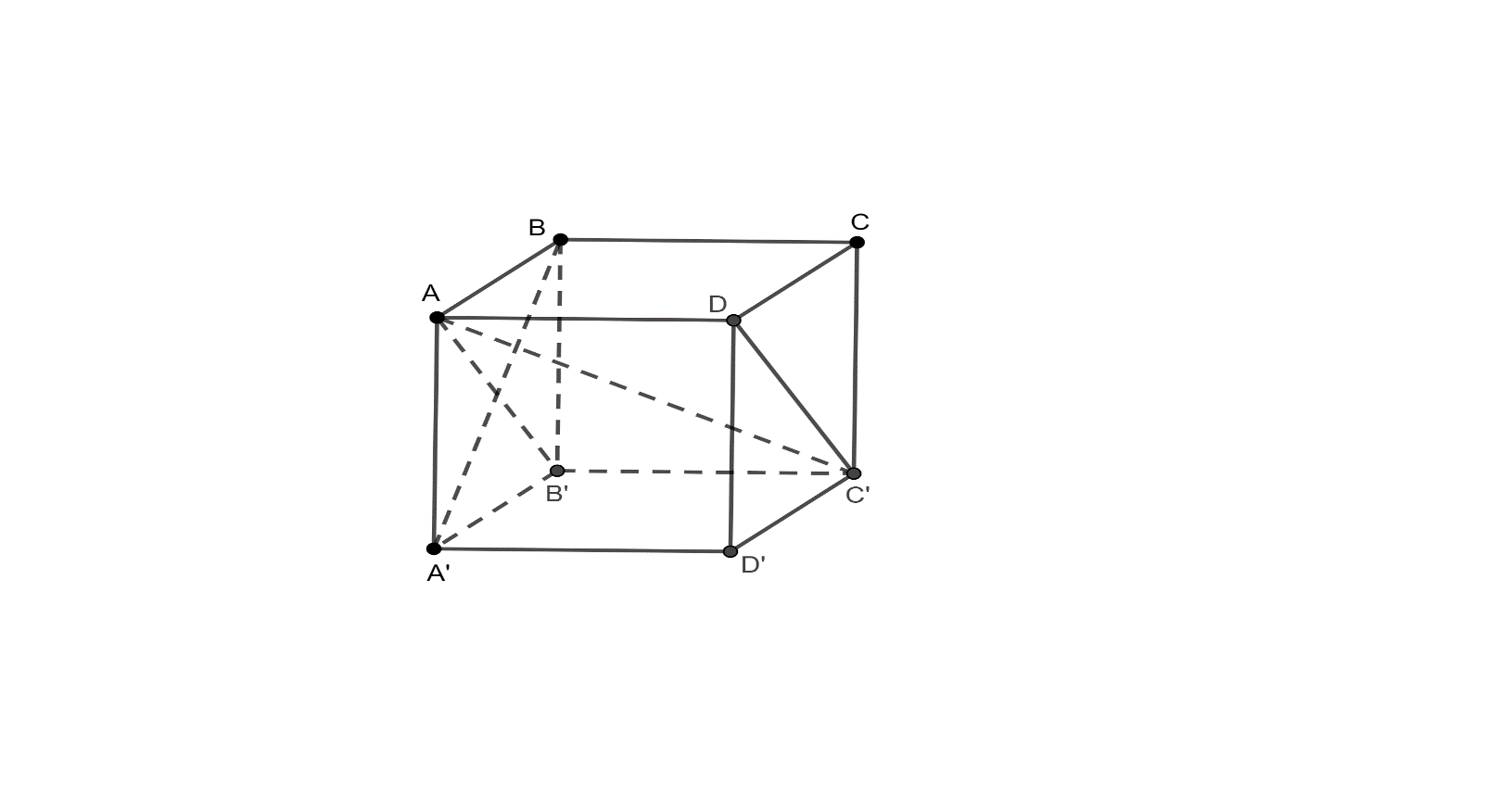
Cho hình lập phương \[ABCD.A'B'C'D'\], có cạnh \(a\).

a) \[\overrightarrow {AD'} .\overrightarrow {CC'} = {a^2}\].

b) \[\overrightarrow {AD'} .\overrightarrow {AB'} = {a^2}\].

c) \[\overrightarrow {AB'} .\overrightarrow {CD'} = 0\].

d) \[\left| {\overrightarrow {AC'} } \right| = a\sqrt 3 \].

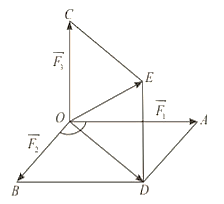
a) Có \(OADB\) là hình bình hành nên \(\overrightarrow {BO} + \overrightarrow {BD} = \overrightarrow {BA} \) (quy tắc hình bình hành).

b) Có \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} ;\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OE} \).

Do đó \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OE} \).

c) Vì \(OADB\) là hình bình hành và \(\widehat {BOA} = 120^\circ \Rightarrow \widehat {OBD} = 60^\circ \).

Xét \(\Delta OBD\) có \(OD = \sqrt {O{B^2} + B{D^2} - 2.OB.BD.\cos 60^\circ } = \sqrt {{{24}^2} + {{12}^2} - 2.24.12.\cos 60^\circ } = 12\sqrt 3 \) N.

d) Ta có \(\Delta OCE\) vuông tại \(C\), ta có \(OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {{6^2} + {{\left( {12\sqrt 3 } \right)}^2}} = 6\sqrt {13} \) N.

Đáp án: a) Sai;   b) Đúng;   c) Sai;   d) Đúng.

Ta có \[\overrightarrow {AB} - \overrightarrow {EH} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \]. Chọn C.