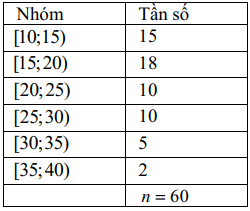
Gọi \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của một mẫu số liệu ghép nhóm. Khi đó khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu trên được xác định bởi công thức
Quảng cáo
Trả lời:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \[{\Delta _Q}\; = {Q_3}--{Q_1}\;\]. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số phần tử của mẫu là \(n = 11 + 10 + 13 + 9 + 7 = 50\).
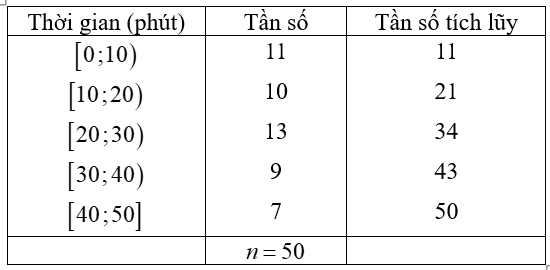
Ta có \(\frac{n}{4} = 12,5\). Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 12,5 nên nhóm này chứa tứ phân vị thứ nhất.
Áp dụng công thức ta có tứ phân vị thứ nhất là \({Q_1} = 10 + \left( {\frac{{12,5 - 11}}{{10}}} \right) \cdot 10 = 11,5\)(phút).
Ta có \(\frac{{3n}}{4} = 37,5\). Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 37,5 nên nhóm này chứa tứ phân vị thứ ba.
Áp dụng công thức ta có tứ phân vị thứ ba là \({Q_3} = 30 + \left( {\frac{{37,5 - 34}}{9}} \right) \cdot 10 = \frac{{305}}{9}\) (phút).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là: \({{\rm{\Delta }}_Q} = {Q_3} - {Q_1} = \frac{{305}}{9} - 11,5 \approx 22,4\)(phút).
Trả lời: 22,4.
Câu 2
Lời giải
Khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp \(12A\)là: \({R_1} = 180 - 150 = 30\) (cm).
Trong mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp \(12B\), khoảng đầu tiên chứa dữ liệu là [155; 160) và khoảng cuối cùng chứa dữ liệu là [175; 180).
Khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn học sinh nữ lớp \(12B\)là: \({R_2} = 180 - 155 = 25\) (cm). Chọn A.
Câu 3
A. \(36;\,\,21,45\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Bạn Trang thống kê lại chiều cao (đơn vị cm) của các bạn học sinh nữ lớp 12C và 12D ở bảng sau.
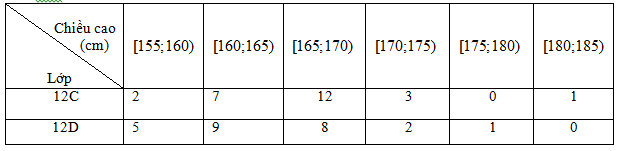
a) Chiều cao cao nhất của các bạn học sinh trong lớp 12D là 185(cm).
b) Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12C là 30(cm).
c) Khoảng biến thiên của chiều cao các bạn học sinh nữ lớp 12D là 25(cm).
d) Chiều cao của học sinh lớp 12C có độ phân tán bé hơn.
Bạn Trang thống kê lại chiều cao (đơn vị cm) của các bạn học sinh nữ lớp 12C và 12D ở bảng sau.

a) Chiều cao cao nhất của các bạn học sinh trong lớp 12D là 185(cm).
b) Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12C là 30(cm).
c) Khoảng biến thiên của chiều cao các bạn học sinh nữ lớp 12D là 25(cm).
d) Chiều cao của học sinh lớp 12C có độ phân tán bé hơn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \({\Delta _Q} = \frac{{11}}{6}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.