Cho hình chóp tứ giác đều \[S.ABCD\]có độ dài tất cả các cạnh bằng \(a\). Tính các tích vô hướng sau:
a) \(\overrightarrow {AS} .\overrightarrow {BC} \)
b) \(\overrightarrow {AS} .\overrightarrow {AC} \).
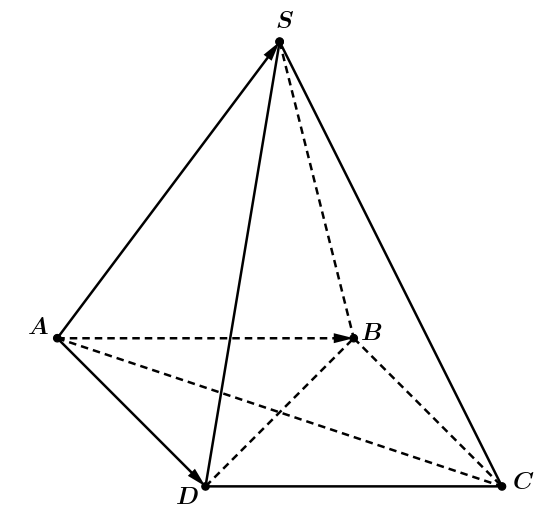
Cho hình chóp tứ giác đều \[S.ABCD\]có độ dài tất cả các cạnh bằng \(a\). Tính các tích vô hướng sau:
a) \(\overrightarrow {AS} .\overrightarrow {BC} \)
b) \(\overrightarrow {AS} .\overrightarrow {AC} \).

Quảng cáo
Trả lời:
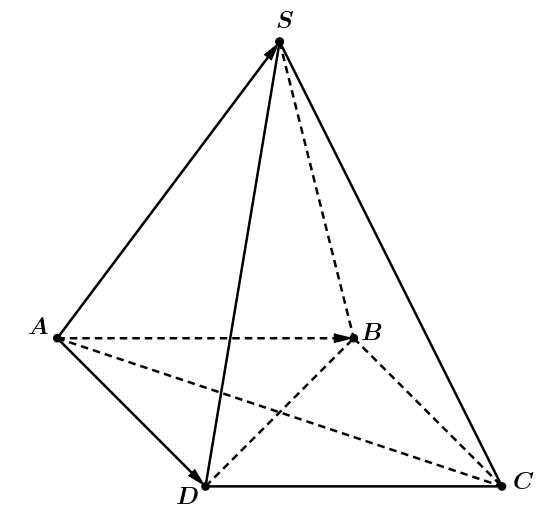
a) Tam giác \(SAD\) có ba cạnh bằng nhau nên là tam giác đều suy ra \(\widehat {SAD} = 60^\circ \).
Tứ giác \(ABCD\) là hình vuông nên \(\overrightarrow {AD} = \overrightarrow {BC} \) suy ra \(\left( {\overrightarrow {AS} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AS} ,\overrightarrow {AD} } \right) = \widehat {SAD} = 60^\circ \).
Do đó \(\overrightarrow {AS} .\overrightarrow {BC} = \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {BC} } \right|.\cos 60^\circ = a.a.\frac{1}{2} = \frac{{{a^2}}}{2}\).
b) Tứ giác \[ABCD\] là hình vuông có độ dài mỗi cạnh là \(a\) nên độ dài đường chéo \[AC\] là \(\sqrt 2 a\).
Tam giác \[SAC\] có \(SA = SC = a\) và \(AC = \sqrt 2 a\) nên tam giác \[SAC\] vuông cân tại \(S\)
Suy ra \(\widehat {SAC} = 45^\circ \), do đó \(\overrightarrow {AS} .\overrightarrow {AC} = \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \widehat {SAC} = a.\sqrt 2 a.\frac{{\sqrt 2 }}{2} = {a^2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
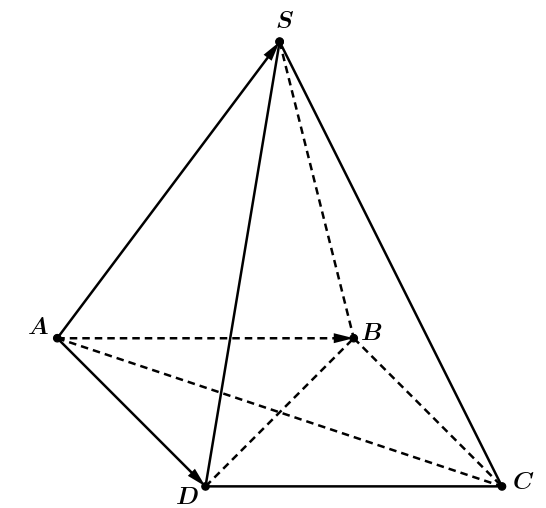
Ta có \[\overrightarrow {AB} = \left( {3;\,\,0;\,\,0} \right)\]. Gọi \(C\left( {x;\,y;\,\,z} \right) \Rightarrow \overrightarrow {DC} = \left( {x;\,\,y - 3;\,\,z} \right)\).
\(ABCD\) là hình bình hành \[ \Rightarrow \overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left( {x;\,\,y - 3;\,\,z} \right) = \left( {3;\,\,0;\,\,0} \right) \Rightarrow C\left( {3;\,\,3;\,\,0} \right)\]
Ta có \(\overrightarrow {AD} = \left( {0;\,\,3;\,\,0} \right)\). Gọi \(A'\left( {x';\,\,y';\,\,z'} \right) \Rightarrow \overrightarrow {A'D'} = \left( { - x';\,\,3 - y';\,\, - 3 - z'} \right)\)
\(ADD'A'\) là hình bình hành \( \Rightarrow \overrightarrow {AD} = \overrightarrow {A'D'} \Rightarrow \left( {x';\,\,y';\,\,z'} \right) = \left( {0;\,\,0;\,\, - 3} \right) \Rightarrow A'\left( {0;\,\,0;\, - 3} \right)\).
Gọi \(B'\left( {{x_0};\,\,{y_0};\,\,{z_0}} \right) \Rightarrow \overrightarrow {A'B'} = \left( {{x_0};\,\,{y_0};\,\,{z_0} + 3} \right)\)
\(ABB'A'\) là hình bình hành \( \Rightarrow \overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow \left( {{x_0};\,\,{y_0};\,\,{z_0}} \right) = \left( {3;\,\,0;\, - 3} \right) \Rightarrow B'\left( {3;\,\,0;\, - 3} \right)\)
\(G\) là trọng tâm tam giác \(A'B'C\) \[ \Rightarrow \left\{ \begin{array}{l}{x_G} = \frac{{0 + 3 + 3}}{3} = 2\\{y_G} = \frac{{0 + 0 + 3}}{3} = 1\\{z_G} = \frac{{ - 3 - 3 + 0}}{3} = - 2\end{array} \right. \Rightarrow G\left( {2;\,\,1;\,\, - 2} \right)\].
Lời giải
Số cá giống mà ông thanh đã thả trong vụ vừa qua là \(50.20 = 1000\left( {{\rm{con}}} \right)\)
Khối lượng trung bình mỗi con cá thành phần trong vụ vừa qua là: \(1500:1000 = 1,5\left( {{\rm{kg}}} \right)\).
Gọi số cá giống cần thả ít đi trong vụ này là: \(x\left( {{\rm{con}}} \right),\left( {x > 0} \right)\)
Theo đề, giảm 8 con thì mỗi con tăng thêm \(0,5\;{\rm{kg/con}}\)
Vậy giảm \(x\) con thì mỗi con tăng thêm \(0,0625x{\rm{ kg/con}}\).
Tổng số lượng cá thu được ở vụ này:
\(F\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right) = - 0,0625{x^2} + 61x + 1500\).
Bài toán trở thành tìm x để \(F\left( x \right)\) đạt giá trị lớn nhất.
Ta có:\(F'\left( x \right) = - 0,125x + 61\)
\(F'\left( x \right) = 0 \Leftrightarrow - 0,125x + 61 = 0 \Leftrightarrow x = 488\)
Bảng biến thiên
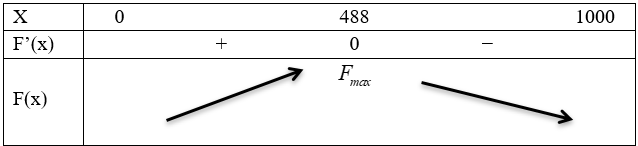
Vậy ông thanh phải thả số cá giống trong vụ này là: \(1000 - 488 = 512\;{\rm{con}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.