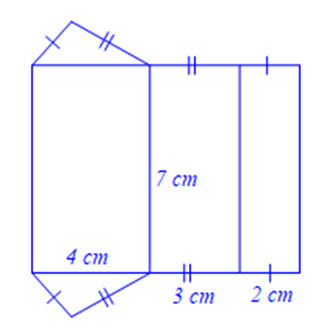
(a) Cho hình lăng trụ đứng có đáy là tam giác vuông có hai cạnh góc vuông là \({\rm{3}}\,\,{\rm{cm}}\) và \({\rm{4}}\,\,{\rm{cm}}\), cạnh huyền là \({\rm{5}}\,\,{\rm{cm}}\). Tính diện tích tất cả các mặt và thể tích của hình lăng trụ đứng đó biết lăng trụ đứng có chiều cao là \({\rm{6}}\,\,{\rm{cm}}\).
(b) Một khối gỗ hình lăng trụ đứng tứ giác có đáy là hình chữ nhật có kích thước là \({\rm{5}}\,\,{\rm{dm}}\), \(6\,\,{\rm{dm}}\) và chiều cao \(7\,\,{\rm{dm}}{\rm{.}}\) Người ta khoét từ đáy một cái lỗ hình lăng trụ đứng tam giác, đáy là một tam giác vuông có hai cạnh góc vuông là \(3\,\,{\rm{dm}}\), \(4\,\,{\rm{dm}}\) và cạnh huyền là \(5\,\,{\rm{dm}}\).
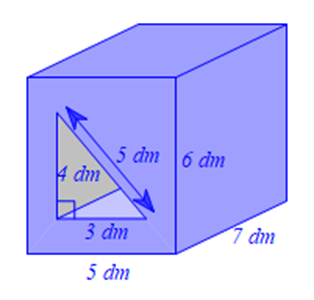
(i) Tính thể tích của khối gỗ sau khi khoét.
(ii) Người ta cần sơn toàn bộ các mặt của khối gỗ, tính diện tích bề mặt cần sơn.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Học sinh vẽ hình đúng số đo góc.
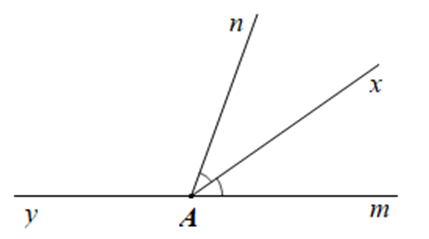
Các cặp góc kề bù (không tính góc bẹt) là: \[\widehat {mAx}\] và \(\widehat {xAy}\); \(\widehat {mAn}\) và \(\widehat {nAy}\).
b) Vì tia \(Ax\) là tia phân giác của \(\widehat {mAn}\) nên: \[\widehat {mAx} = \widehat {xAn} = \frac{1}{2}\widehat {mAn} = \frac{1}{2}\,\,.\,70^\circ = 35^\circ \].
Ta có \(\widehat {mAx} + \widehat {xAy} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {xAy} = 180^\circ - \widehat {mAx} = 180^\circ - 35^\circ = 145^\circ .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1. a) \[\frac{{ - 2}}{3} + \frac{4}{5}\, + \frac{{ - 5}}{3} - \frac{{19}}{5} = \left( {\frac{{ - 2}}{3} + \frac{{ - 5}}{3}} \right) + \left( {\frac{4}{5}\, - \frac{{19}}{5}} \right)\]
\[ = \frac{{ - 7}}{3} + \left( { - 3} \right) = \frac{{ - 7}}{3} - \frac{9}{3} = \frac{{ - 16}}{3}\].
b) \[12\,\,.\,\,{\left( {\frac{3}{2}} \right)^2} + {\left( {\frac{{25}}{6}} \right)^0}\,\,.\,\,\frac{{15}}{2} - 9\frac{1}{4} = 12\,\,.\,\,\frac{9}{4} + 1\,\,.\,\,\frac{{15}}{2} - \frac{{37}}{4}\]
\[ = 12\,\,.\,\,\frac{9}{4} + 1\,\,.\,\,\frac{{15}}{2} - \frac{{37}}{4} = 27 + \frac{{15}}{2} - \frac{{37}}{4} = \frac{{69}}{2} - \frac{{37}}{4} = \frac{{101}}{4}\].
2. a) \(\frac{{ - 3}}{8} + \frac{5}{6}x = \frac{{ - 17}}{{12}}\)
\(\frac{5}{6}x = \frac{{ - 17}}{{12}} + \frac{3}{8}\)
\(\frac{5}{6}x = \frac{{ - 25}}{{24}}\)
\(x = \frac{{ - 25}}{{24}}:\frac{5}{6}\)
\(x = \frac{{ - 5}}{4}\).
Vậy \(x = \frac{{ - 5}}{4}\).
b) \({\left( {\frac{1}{2}} \right)^3} - \left( {x + \frac{2}{5}} \right)\,:\frac{2}{3} = \frac{{ - 31}}{{40}}\)
\(\frac{1}{8} - \left( {x + \frac{2}{5}} \right)\,\,\,.\,\,\frac{3}{2} = \frac{{ - 31}}{{40}}\)
\(\left( {x + \frac{2}{5}} \right)\,\,\,.\,\,\frac{3}{2} = \frac{1}{8} + \frac{{31}}{{40}}\)
\(\left( {x + \frac{2}{5}} \right)\,\,\,.\,\,\frac{3}{2} = \frac{9}{{10}}\)
\(x + \frac{2}{5}\, = \frac{9}{{10}}:\,\frac{3}{2}\)
\(x + \frac{2}{5}\, = \frac{3}{5}\)
\(x\, = \frac{3}{5} - \frac{2}{5}\)
\(x\, = \frac{1}{5}\)
Vậy \(x\, = \frac{1}{5}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(12\,\,{\rm{cm}}\)
\(11\,\,{\rm{cm}}\)
\(9\,\,{\rm{cm}}\)
\(22\,\,{\rm{cm}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(1\,\,{\rm{cm}}\)
\(2\,\,{\rm{cm}}\)
\(3\,\,{\rm{cm}}\)
\(4\,\,{\rm{cm}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập