Cho hình vẽ bên.
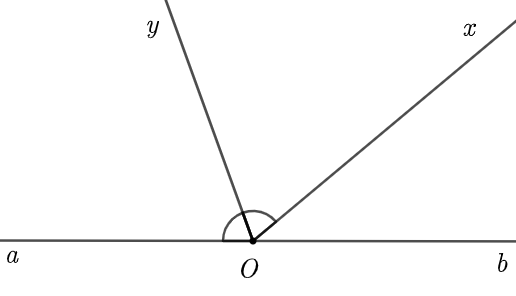
(a) Tìm tia phân giác của \(\widehat {aOx}\).
(b) Cho \(\widehat {bOx} = 40^\circ \), \(\widehat {aOb}\) là góc bẹt. Tính \(\widehat {xOy}.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Trong hình vẽ ta thấy:
• Tia \(Oy\) nằm giữa hai tia \(Oa\) và \(Ox\);
• \(\widehat {aOy} = \widehat {xOy}\)
Do đó \(Oy\) là tia phân giác của \(\widehat {aOx}\).
b) Ta có \(\widehat {aOx}\) và \(\widehat {bOx}\) là hai góc kề bù (vì \(\widehat {aOb}\) là góc bẹt).
Khi đó \(\widehat {aOx} + \widehat {bOx} = 180^\circ \).
Suy ra \(\widehat {aOx} = 180^\circ - \widehat {bOx} = 180^\circ - 40^\circ = 140^\circ \).
Vì \(Oy\) là tia phân giác của \(\widehat {aOx}\) (câu a) nên:
\(\widehat {aOy} = \widehat {xOy} = \frac{{\widehat {aOx}}}{2} = \frac{{140^\circ }}{2} = 70^\circ \).
Vậy \(\widehat {xOy} = 70^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tiền điện nhà bạn Kiên phải trả thuộc ba bậc như sau:
Bậc 1. Từ 0 đến 50 kWh (50 kWh).
Bậc 2. Từ 51 đến 100 kWh (50 kWh).
Bậc 3. Từ 101 đến 200 kWh (100 kWh).
Bậc 4. Từ 201 đến 280 kWh (80 kWh).
Khi đó, ta tính được như sau:
Giá tiền của 50 kWh điện bậc 1 là:
\(1678\,\,.\,\,50 = 83\,\,900\) (đồng)
Giá tiền của 50 kWh điện bậc 2 là:
\(1734\,\,.\,\,50 = 86\,\,700\) (đồng)
Giá tiền của 100 kWh điện bậc 3 là:
\(2014\,\,.\,\,100 = 20\,1\,\,400\) (đồng)
Giá tiền của 80 kWh điện bậc 4 là:
\(2536\,\,.\,\,80 = 20\,2\,\,880\) (đồng)
Tiền điện của 280 kWh điện nhà Kiên là:
\(83\,\,900 + 86\,\,700 + 201\,\,400 + 202\,\,880 = 574\,\,\,880\) (đồng)
Tiền thuế GTGT cần phải trả là:
\(574\,\,\,880\,\,.\,\,10\% = 57\,\,4\,88\) (đồng)
Tổng số tiền nhà Kiên cần trả là:
\(574\,\,\,880 + 57\,\,4\,88 = 632\,\,368\) (đồng).
Vậy tổng tiền điện nhà Dung cần trả là \(632\,\,368\) đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Diện tích xung quanh của hộp sữa có dạng hình hộp chữ nhật là:
\(5\,\,.\,\,4\,\,.\,\,8 = 160\) (cm2).
Vậy diện tích xung quanh của hộp sữa là 160 cm2.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
3125
1
1225
1525.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập