Cho hình vẽ bên.
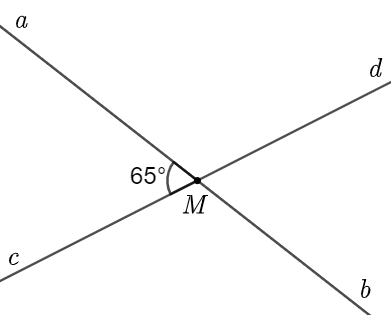
(a) Kể tên các góc kề bù với \(\widehat {aOc}\).
(b) Tính số đo các góc \(\widehat {aOd},\,\,\widehat {bOc},\,\,\widehat {bOd}\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:

a) Các góc kề bù với \(\widehat {aOc}\) là: \(\widehat {aOd},\,\,\widehat {bOc}\).
b) Vì \(\widehat {aOc}\) và \(\widehat {aOd}\) là hai góc kề bù nên
\(\widehat {aOc} + \widehat {aOd} = 180^\circ \)
Suy ra \(\widehat {aOd} = 180^\circ - \widehat {aOc} = 180^\circ - 65^\circ = 115^\circ \).
• \(\widehat {aOd} = \widehat {bOc} = 115^\circ \) (hai góc đối đỉnh);
• \(\widehat {aOc} = \widehat {bOd} = 65^\circ \) (hai góc đối đỉnh).
Vậy \(\widehat {aOd} = 115^\circ ,\,\,\widehat {bOc} = 115^\circ ,\,\,\widehat {bOd} = 65^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích xung quanh bên trong lòng hồ bơi là:
\(2\,\,.\,\,\left( {12 + 8} \right)\,\,.\,\,3 = 120\) (m2).
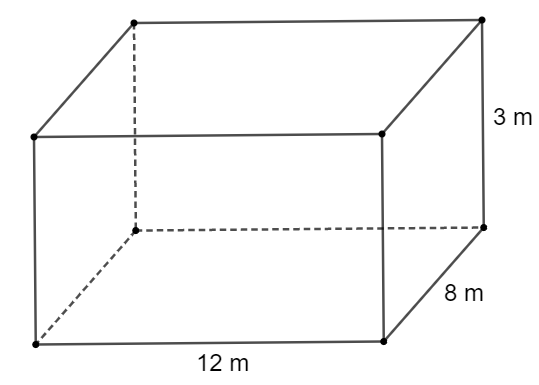
Diện tích đáy của hồ bơi là:
\(12\,\,.\,\,8 = 96\) (m2).
Diện tích các mặt trong lòng hồ bơi cần lát gạch là:
\(120 + 96 = 216\) (m2).
Đổi: 50 cm = 0,5 m.
Số viên gạch cần mua ít nhất để lát bên trong hồ bơi là:
\(216:0,5 = 432\) (viên gạch).
Vậy để lát bên trong hồ bơi cần mua ít nhất 432 viên gạch.
Lời giải
Đáp án đúng là: B
• Hai góc kề bù thì có tổng số đo bằng \[180^\circ \] nên (I) đúng.
• Tổng số đo hai góc đã cho là \(100^\circ + 100^\circ = 200^\circ \ne 180^\circ \), nên (II) sai.
• Hai góc có tổng số đo bằng \(180^\circ \) là hai góc bù nhau nhưng chưa chắc ở vị trí kề nhau nên hai góc có tổng số đo bằng \(180^\circ \) chưa chắc là hai góc kề bù. Do đó (III) sai.
Vậy chỉ có ý (I) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.