Tìm giá trị lớn nhất của biểu thức \(A =  - {x^2} + 2xy - 4{y^2} + 2x + 10y - 3.\)

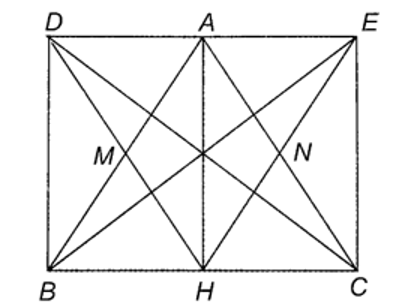
a) • Tứ giác \[AHBD\] có \[M\] là trung điểm của \[AB\] và \[HD\] nên là hình bình hành.

Do \[AH\] là đường cao của \[\Delta ABC\] nên \[AH \bot BC\], suy ra \[\widehat {AHB} = 90^\circ \].

Hình bình hành \[AHBD\] có \[\widehat {AHB} = 90^\circ \] nên \[AHBD\] là hình chữ nhật.

• Tương tự, tứ giác \[AHCE\] có \[N\] là trung điểm của \[AC\] và \[HE\] nên là hình bình hành.

Lại có \[\widehat {AHC} = 90^\circ \] nên \[AHCE\] là hình chữ nhật.

• Do \[AHBD,{\rm{ }}AHCE\] là các hình chữ nhật (chứng minh trên)

Suy ra \[\widehat {ADB} = \widehat {DBH} = \widehat {HCE} = \widehat {AEC} = 90^\circ \].

Tứ giác \[BCED\] có \[\widehat {ADB} = \widehat {DBH} = \widehat {HCE} = \widehat {AEC} = 90^\circ \] là các góc ở đỉnh nên \[BCED\] là hình chữ nhật.

b) Vì \[ADBH,{\rm{ }}AECH\] là các hình chữ nhật nên \[AD = BH,{\rm{ }}AE = HC,{\rm{ }}AD{\rm{ // }}BC,{\rm{ }}AE{\rm{ // }}BC\].

Mà \[\Delta ABC\] cân tại \[A\] có \[AH\] là đường cao nên đồng thời là đường trung tuyến, do đó \[H\] là trung điểm của \[BC\], suy ra \[BH = HC\].

Từ đó, \[AD = BH = HC = AE\].

Tứ giác \[ADHC\] có: \[AD{\rm{ // }}HC,{\rm{ }}AD = HC\] nên \[ADHC\] là hình bình hành.

Tứ giác \[ABHE\] có: \[AE{\rm{ // }}BH,{\rm{ }}AE = BH\] nên \[ABHE\] là hình bình hành.

Vì \[ADHC\] là hình bình hành nên \[CD\] cắt \[AH\] tại trung điểm của \[AH\].

Vì \[AEHB\] là hình bình hành nên \[BE\] cắt \[AH\] tại trung điểm của \[AH\].

Vậy giao điểm của \[BE\] và \[CD\] là trung điểm của \[AH\].

c) Do \[BCED\] là hình chữ nhật (chứng minh câu a) nên \[CD = BE\] (hai đường chéo bằng nhau).

Do \[AHBD,{\rm{ }}AHCE\] là các hình chữ nhật nên \[AB = DH,{\rm{ }}AC = HE\] (hai đường chéo bằng nhau).

Mà \[AB = AC\] (do \[\Delta ABC\] cân tại \[A\]) nên \[DH = HE\].