Xét hai hình bình hành \[MNBA\] và \[MNCB\].

a) Chứng minh \[B\] là trung điểm của \[AC\].

b) Hỏi tam giác \[MAB\] thoả mãn điều kiện gì để \[MNCA\] là một hình thang cân?

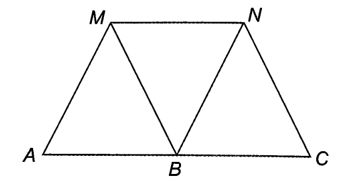
a) Do \[MNBA\] và \[MNCB\] là hình bình hành

Suy ra \[AB{\rm{ // }}MN,{\rm{ }}BC{\rm{ // }}MN\] nên theo tiên đề Euclid, hai đường thẳng \[AB\] và \[BC\] trùng nhau.

Do đó ba điểm \[A,{\rm{ }}B,{\rm{ }}C\] thẳng hàng.

Do \[MNBA\] và \[MNCB\] là hình bình hành nên \[AB = MN,{\rm{ }}BC = MN\]. Suy ra \(AB = BC\).

Mà \[A,{\rm{ }}B,{\rm{ }}C\] thẳng hàng nên \[B\] là trung điểm của \[AC\].

b) Từ câu a, ta suy ra \(MN{\rm{//}}\,AC\) nên \[MNCA\] là hình thang.

Do \[MNCB\] là hình bình hành nên \[NC{\rm{ // }}MB\], từ đó \[\widehat {NCB} = \widehat {MBA}\] (hai góc đồng vị). Điều kiện để hình thang \[MNCA\] là hình thang cân là \[\widehat {MAB} = \widehat {NCB}\] tức là \[\widehat {MAB} = \widehat {MBA}.\]

Vậy điều kiện để \[MNCA\] là hình thang cân là tam giác \[MAB\] cân tại \[M\].

c) 

Chứng minh tương tự câu a, ta có \(MN\,{\rm{//}}\,AD\) và bốn điểm \(A,\,B,\,C,\,D\) thẳng hàng. Do đó \[MNDA\] là hình thang.

Do \[MNDC\] là hình bình hành nên \[ND{\rm{ // }}MC\], từ đó \[\widehat {NDC} = \widehat {MCA}\] (hai góc đồng vị). Điều kiện để hình thang \[MNDA\] là hình thang cân là \[\widehat {NDC} = \widehat {MAC}\].

Khi đó điều kiện để \[MNDA\] là hình thang cân là \[\widehat {MCA} = \widehat {MAC}\] tức là tam giác \[MAC\] cân tại \[M\].

Do \[MB\] là đường trung tuyến của tam giác \[MAC\] nên điều kiện để tam giác \[MAC\] cân tại \[M\] là \[MB\] vuông góc với \[AC\].

Vậy điều kiện để hình thang \[MNDA\] là hình thang cân đó là tam giác \[MAB\] vuông tại \[B\].