Số tự nhiên \[x\] nhỏ nhất thỏa mãn điều kiện \[x\] chia cho \[12;{\rm{ }}15\]đều dư \[1\] là
\[31\]
\[61\]
\[91\]
\[121\].
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
Vì \((x - 1)\,\, \vdots \,\,12;\,\,(x - 1)\,\, \vdots \,\,15\) mà \[x\] nhỏ nhất nên \[x - 1\] là \[BCNN\left( {12,\,\,15} \right)\].
Mà \[BCNN\left( {12,\,\,15} \right) = 60\]. Vậy \[x = 61\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
18 cm
27 cm
36 cm
54 cm.
Lời giải
Đáp án đúng là: A
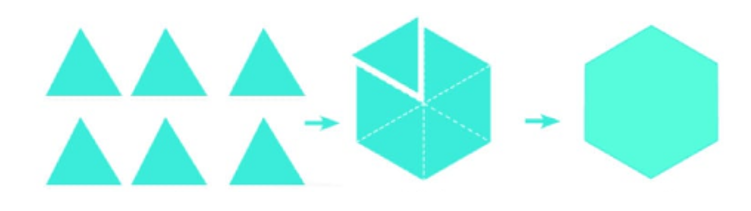
Chu vi một tam giác đều là \(9\,\,{\rm{cm}}\) nên độ dài một cạnh của tam giác đều là \(3\,\,{\rm{cm}}\).
Khi xếp thành hình lục giác đều, mỗi cạnh của hình lục giác đều là một cạnh của tam giác đều. Do có chu vi hình lục giác đều là \[3\,\,.\,\,6 = 18\,\,({\rm{cm}})\].
Câu 2
\(\left\{ {1;\,\,17;\,\,0} \right\}\)
\(\left\{ 1 \right\}\)
\(\left\{ {17} \right\}\)
\(\left\{ {1;\,\,17} \right\}\).
Lời giải
Đáp án đúng là: D
Tập hợp các ước của \(17\) là: Ư\(\left( {17} \right) = \left\{ {1;\,\,17} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(a \notin M\)
\(y \in M\)
\(1 \in M\)
\(b \notin M\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.