Một đội thiếu niên khi xếp hàng \[2\,;\,\,3\,;\,\,4\,;\,\,5\] đều thừa một người. Biết số đội viên trong khoảng 100 đến 150 người. Tính số đội viên thiếu niên của đội.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x\) (đội viên) là số đội viên của đội \(\left( {x \in \mathbb{N}*;\,\,100 < x < 150} \right)\).
Vì khi xếp hàng \[2\,;\,\,3\,;\,\,4\,;\,\,5\] đều thừa một người nên \[x--1\] đội viên khi xếp hàng \[2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5\] thì vừa đủ.
• Khi đội xếp thành hàng 2 thì vừa đủ nên \[x-1\] là bội của 2;
• Khi đội xếp thành hàng 3 thì vừa đủ nên \[x-1\] là bội của 3;
• Khi đội xếp thành hàng 4 thì vừa đủ nên \[x-1\] là bội của 4;
• Khi đội xếp thành hàng 5 thì vừa đủ nên \[x-1\] là bội của 5.
Do đó \[x--1\] là \[BC\left( {2,\,\,3,\,\,4,\,\,5} \right)\].
Ta có: \[2 = 2;{\rm{ }}3 = 3;{\rm{ }}4 = {2^2};{\rm{ }}5 = 5\].
\(BCNN\left( {2,\,\,3,\,\,4,\,\,5} \right) = 3\,\,.\,\,5\,\,.\,\,{2^2} = 3\,\,.\,\,5\,\,.\,\,4 = 60\) .
\(BC\left( {2,\,\,3,\,\,4,\,\,5} \right) = \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,...} \right\}\).
Vì \[100 < x < 150\] nên \[99 < x-1 < 149\].
Do đó \[x-1 = 120\] nên \[x = 121\].
Vậy đội có 121 đội viên.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
\[1 \notin A\]
\[3 \in A\]
\[6 \notin B\]
\[5 \in A\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
• Tập hợp \(A\) gồm các phần tử: \[2;\;4;\;6\].
• Tập hợp \(B\) gồm các phần tử: \[1;\;2;\;3;\;4;\;5;\,6\].
Do đó, phương án đúng là \[1 \notin A\].
Câu 2
\[11\]
\[13\]
\[14\]
\[12\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Vì \[13;{\rm{ }}61\]chia \[x\] dư \[1\] nên \[13 - 1\] và \[61 - 1\] chia hết cho \[x\].
Hay \[12\] và \[60\] chia hết cho \[x\], mà \[x\] lớn nhất nên \[x\] là ƯCLN\[\left( {12,\,\,600} \right)\].
Vậy \[x = 12\].
Câu 3
\(24:4 - {1^{123}}\)
\({5^3}:{5^2} + {2022^0}\)
\(6 - {(6 - 5)^2}\,.\,\,2\)
\(\left[ {\left( {15 - 3} \right):3 + {9^0}} \right]\,\,.\,\,2\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(AB,CD,AC\)
\(AD,FC,EB\)
\(AB,CD,EF\)
\(FE,ED,DC\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
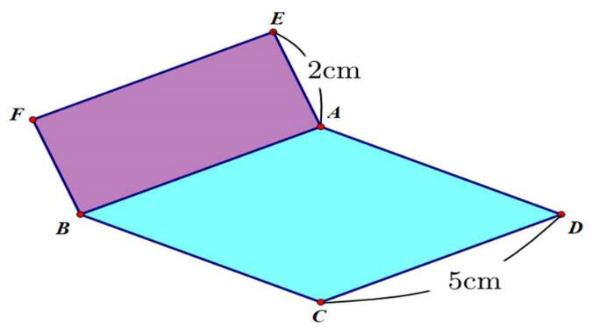
\(14\;\,\,{\rm{c}}{{\rm{m}}^2}\)
\(7\;\,\,{\rm{c}}{{\rm{m}}^2}\)
\(10\;\,\,{\rm{c}}{{\rm{m}}^2}\)
\(5\;\,\,{\rm{c}}{{\rm{m}}^2}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập