Một nhà từ thiện muốn chia \(40\) cái bánh trung thu, \(60\) cây lồng đèn và \(80\) hộp sữa thành các phần quà, sao cho mỗi phần quà có số bánh, lồng đèn và hộp sữa bằng nhau. Hỏi có thể chia được nhiều nhất bao nhiêu phần quà?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Số phần quà được chia phải là ước của cả \(40;\,\,60\) và \(80\).
Số phần quà được chia phải là nhiều nhất có thể.
Vì vậy, số phần quà được chia là ước chung lớn nhất của \(40;\,\,60\) và \(80\).
Ta có ƯCLN\(\left( {40,\,\,60,\,\,80} \right) = 20\).
Vậy có thể chia được nhiều nhất 20 phần quà.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \(2A = 2 + {2^2} + {2^3} + {2^4} + ... + {2^{2023}}\).
\( \Rightarrow 2A - A = \left( {2 + {2^2} + {2^3} + ... + {2^{2023}}} \right) - \left( {1 + 2 + {2^2} + ... + {2^{2022}}} \right)\)
\( = 2 + {2^2} + {2^3} + ... + {2^{2023}} - 1 - 2 - {2^2} - ... - {2^{2022}}\)
\[ = {2^{2023}} + ({2^{2022}} - {2^{2022}}) + ... + ({2^3} - {2^3}) + ({2^2} - {2^2}) + (2 - 2) - 1\]
\( = {2^{2023}} - 1\).
Từ đó tính được \(B = {2^{2023}} - A = {2^{2023}} - \left( {{2^{2023}} - 1} \right) = {2^{2023}} - {2^{2023}} + 1 = 1\).
Vậy \(B = 1\).
Lời giải
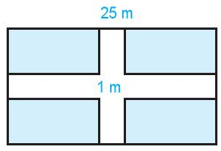
Nhìn vào hình vẽ ta thấy diện tích đất trồng cây là 4 mảnh đất hình chữ nhật nhỏ có kích thước như nhau.
Chiều dài của mỗi mảnh đất nhỏ màu xanh là: \[\left( {25 - 1} \right):2 = 12\] (m).
Chiều rộng của mỗi mảnh đất nhỏ màu xanh là: \[\left( {15 - 1} \right):2 = 7\] (m).
Diện tích của mỗi mảnh đất nhỏ màu xanh là: \[12\,\,.{\rm{ }}7 = 84\,\,({{\rm{m}}^2})\].
Diện tích đất để trồng cây là: \[4\,\,.\,\,84 = 336\,\,({{\rm{m}}^2})\].
Vậy diện tích đất để trồng cây là \[336\,\,{{\rm{m}}^2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
0; 2; 4; 6; 8
\(1;\,\,3;\,\,5;\,\,7\)
\(0\)
\(0;\,\,2;\,\,4;\,\,6;\,\,8;\,\,...\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Phép chia – phép cộng – lũy thừa
Phép cộng – lũy thừa – phép chia
Lũy thừa – phép cộng – phép chia
Lũy thừa – phép chia – phép cộng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
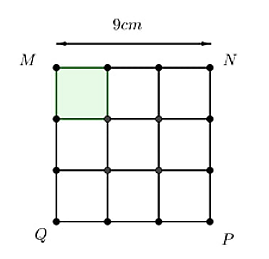
9 cm2
1 cm2
12 cm2
81 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.