Cho \(A = 1 + 2 + {2^2} + {2^3} + ... + {2^{2022}}\).
Tính nhanh giá trị biểu thức: \(B = {2^{2023}} - A\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Ta có: \(2A = 2 + {2^2} + {2^3} + {2^4} + ... + {2^{2023}}\).
\( \Rightarrow 2A - A = \left( {2 + {2^2} + {2^3} + ... + {2^{2023}}} \right) - \left( {1 + 2 + {2^2} + ... + {2^{2022}}} \right)\)
\( = 2 + {2^2} + {2^3} + ... + {2^{2023}} - 1 - 2 - {2^2} - ... - {2^{2022}}\)
\[ = {2^{2023}} + ({2^{2022}} - {2^{2022}}) + ... + ({2^3} - {2^3}) + ({2^2} - {2^2}) + (2 - 2) - 1\]
\( = {2^{2023}} - 1\).
Từ đó tính được \(B = {2^{2023}} - A = {2^{2023}} - \left( {{2^{2023}} - 1} \right) = {2^{2023}} - {2^{2023}} + 1 = 1\).
Vậy \(B = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
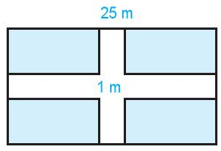
Nhìn vào hình vẽ ta thấy diện tích đất trồng cây là 4 mảnh đất hình chữ nhật nhỏ có kích thước như nhau.
Chiều dài của mỗi mảnh đất nhỏ màu xanh là: \[\left( {25 - 1} \right):2 = 12\] (m).
Chiều rộng của mỗi mảnh đất nhỏ màu xanh là: \[\left( {15 - 1} \right):2 = 7\] (m).
Diện tích của mỗi mảnh đất nhỏ màu xanh là: \[12\,\,.{\rm{ }}7 = 84\,\,({{\rm{m}}^2})\].
Diện tích đất để trồng cây là: \[4\,\,.\,\,84 = 336\,\,({{\rm{m}}^2})\].
Vậy diện tích đất để trồng cây là \[336\,\,{{\rm{m}}^2}\].
Câu 3
0; 2; 4; 6; 8
\(1;\,\,3;\,\,5;\,\,7\)
\(0\)
\(0;\,\,2;\,\,4;\,\,6;\,\,8;\,\,...\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Phép chia – phép cộng – lũy thừa
Phép cộng – lũy thừa – phép chia
Lũy thừa – phép cộng – phép chia
Lũy thừa – phép chia – phép cộng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
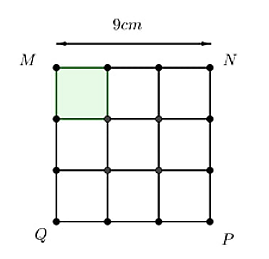
9 cm2
1 cm2
12 cm2
81 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.