PHẦN II. TỰ LUẬN (8,0 điểm)

(1,0 điểm) Tìm \(x,\) biết:

a) \[2{x^2} - 8x = 0.\]

b) \[{x^3} - 6{x^2} + 9x = 0.\]

Hướng dẫn giải

Theo đề bài: \({x^2} + \frac{8}{{{x^2}}} + \frac{{{y^2}}}{8} = 8\) suy ra \(2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = 16\)

Ta có: \[2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = \left( {{x^2} + \frac{{16}}{{{x^2}}} - 8} \right) + \left( {{x^2} + \frac{{{y^2}}}{4} - xy} \right) + xy + 8\]

\[ = {\left( {x - \frac{4}{x}} \right)^2} + {\left( {x - \frac{y}{2}} \right)^2} + xy + 8\].

Vì \[{\left( {x - \frac{4}{x}} \right)^2} \ge 0\,;\,\,{\left( {x - \frac{y}{2}} \right)^2} \ge 0\] nên \[xy + 8 \le 16\] hay \[xy \le 8\].

Suy ra \(A = xy + 2023 \le 8 + 2023 = 2031\).

Dấu xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}{\left( {x - \frac{4}{x}} \right)^2} = 0\\{\left( {x - \frac{y}{2}} \right)^2} = 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x - \frac{4}{x} = 0\\x - \frac{y}{2} = 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}{x^2} = 4\\y = 2x\end{array} \right.\).

Khi đó, \(x = 2\,;\,\,y = 4\) hoặc \(x = - 2\,;\,\,y = - \,4\).

Vậy giá trị lớn nhất của biểu thức \(A\) là 2031 khi \(x = 2\,;\,\,y = 4\) hoặc \(x = - 2\,;\,\,y = - \,4\).

Hướng dẫn giải

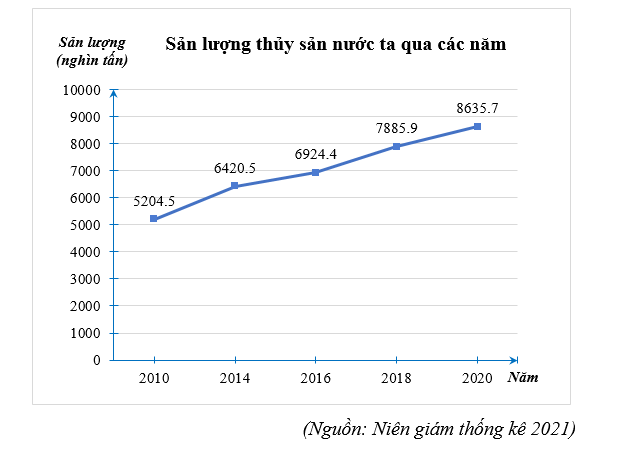
a) Ta có bảng thống kê sản lượng thủy sản nước ta qua các năm 2010; 2014; 2016; 2018; 2020 như sau:

b) Dựa vào thống kê, ta có:

- Năm 2020 sản lượng thủy sản nước ta cao nhất (\[8\,\,635,7\] nghìn tấn).

- Năm 2010 sản lượng thủy sản nước ta thấp nhất (\[5\,\,204,5\] nghìn tấn).

c) Năm 2020 sản lượng thủy sản nước ta nhiều hơn năm 2014 là:

\(8\,\,635,7 - 6\,\,420,5 = 2\,\,215,2\) (nghìn tấn)

Năm 2020 sản lượng thủy sản nước ta gấp số lần so với năm 2014 là:

\(8\,\,635,7:6\,\,420,5 = 1,3\) (lần)

Vậy nhận định của bài báo đó là chính xác.