Số học sinh khối 6 của một trường THCS khi xếp hàng 10 em thì thừa 8 em, xếp hàng 12 em thì thừa 10 em, khi xếp hàng 15 em thì thừa 13 em nhưng khi xếp hàng 17 thì vừa đủ. Tính số học sinh khối 6 của trường biết số học sinh là một số tự nhiên có 3 chữ số nhỏ hơn 250.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Gọi số học sinh của trường THCS đó là \(a\) (học sinh) \(\left( {a \in \mathbb{N},100 \le a < 250} \right)\).
Do khi xếp hàng 10 em thì thừa 8 em nên \(a\) chia 10 dư 8, hay \(\left( {a + 2} \right) \vdots 10\).
Khi xếp hàng 12 em thì thừa 10 em nên \(a\) chia 12 dư 10, hay \(\left( {a + 2} \right) \vdots 12\).
Khi xếp hàng 15 em thì thừa 13 em nên \(a\) chia 15 dư 13, hay \(\left( {a + 2} \right) \vdots 15\).
Từ đó suy ra \(a + 2 \in BC\left( {10,12,15} \right)\).
Ta có: \(10 = 2.5\); \(12 = {2^2}.3\); \(15 = 3.5\).
Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\).
Khi đó \[a + 2 \in BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;240;300;360;...} \right\}\].
Mà \(100 \le a < 250\) nên \(102 \le a + 2 \le 252\), suy ra \(a + 2 \in \left\{ {120;180;240} \right\}\)
Do đó \(a \in \left\{ {118;178;238} \right\}\)
Mặt khác khi số học sinh của trường xếp hàng 17 thì vừa đủ nên \(a \vdots 17\)
Xét 3 trường hợp ở trên ta có \(a = 238\) thỏa mãn.
Vậy trường THCS đó có 238 học sinh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Với \(x,y\) là số nguyên, từ \(\left( {x + 5} \right)\left( {2y + 1} \right) = 4\), suy ra \(2y + 1\) là ước của 4.
Mà Ư\(\left( 4 \right) = \left\{ {1; - 1;2; - 2;4; - 4} \right\}\).
Do \(y\) là số nguyên nên \(2y + 1\) là số lẻ nên \(2y + 1\) chỉ là ước lẻ của 4.
Khi đó \(2y + 1 \in \left\{ {1; - 1} \right\}\).
Ta có bảng sau:
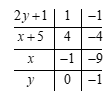
Vậy \[\left( {x;y} \right) \in \left\{ {\left( { - 1;0} \right);\left( { - 9; - 1} \right)} \right\}\].
Lời giải
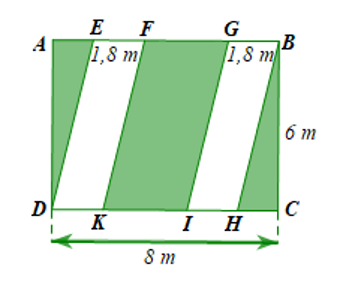
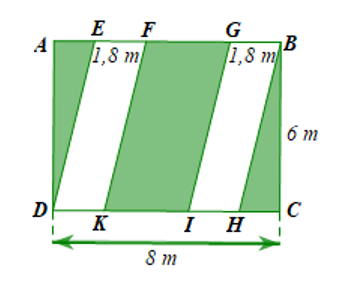
a) Diện tích hình bình hành EFKD và diện tích hình bình hành GBHI bằng nhau.
Diện tích trồng hoa là: \(2.\left( {1,8.6} \right) = 21,6\left( {{m^2}} \right)\).
b) Diện tích mảnh đất là: \(8.6 = 48\left( {{m^2}} \right)\).
Diện tích trồng cỏ là: \(48 - 21,6 = 26,4\left( {{m^2}} \right)\).
Tiền công trả cho trồng hoa là:
\(80\,\,000.21,6 = 1\,\,728\,\,000\) (đồng)
Tiền công trả cho trồng cổ là:
\(60\,\,000.26,4 = 1\,\,584\,\,000\) (đồng).
Tiền công cần chi trả cho trồng cả hoa và cỏ là:
\(1\,\,728\,\,000 + 1\,\,584\,\,000 = 3\,\,312\,\,000\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(x\) chia hết cho 4;
B. \(x\) chia hết cho 2;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(28;19;0; - 36; - 21\);
B. \( - 49; - 40; - 35; - 20;0\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.