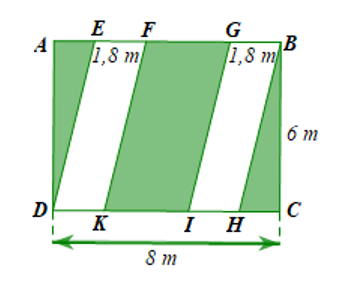
Trên mảnh đất hình chữ nhật có chiều dài \(8\,\,{\rm{m}}\), chiều rộng \(6\,\,{\rm{m}}\), người ta chia phân khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành EFKD và GBHI, cỏ sẽ được trồng ở các phần đất còn lại.
a) Tính diện tích trồng hoa.
b) Tiền công để trả cho mỗi mét vuông trồng hoa là \(80\,\,000\) đồng và cho mỗi mét vuông trồng cỏ là \(60\,\,000\) đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
Trên mảnh đất hình chữ nhật có chiều dài \(8\,\,{\rm{m}}\), chiều rộng \(6\,\,{\rm{m}}\), người ta chia phân khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành EFKD và GBHI, cỏ sẽ được trồng ở các phần đất còn lại.
a) Tính diện tích trồng hoa.
b) Tiền công để trả cho mỗi mét vuông trồng hoa là \(80\,\,000\) đồng và cho mỗi mét vuông trồng cỏ là \(60\,\,000\) đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
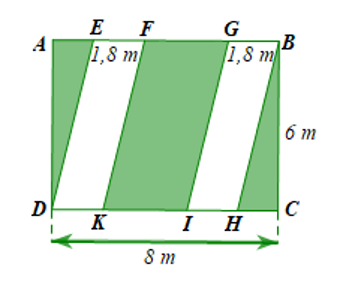
a) Diện tích hình bình hành EFKD và diện tích hình bình hành GBHI bằng nhau.
Diện tích trồng hoa là: \(2.\left( {1,8.6} \right) = 21,6\left( {{m^2}} \right)\).
b) Diện tích mảnh đất là: \(8.6 = 48\left( {{m^2}} \right)\).
Diện tích trồng cỏ là: \(48 - 21,6 = 26,4\left( {{m^2}} \right)\).
Tiền công trả cho trồng hoa là:
\(80\,\,000.21,6 = 1\,\,728\,\,000\) (đồng)
Tiền công trả cho trồng cổ là:
\(60\,\,000.26,4 = 1\,\,584\,\,000\) (đồng).
Tiền công cần chi trả cho trồng cả hoa và cỏ là:
\(1\,\,728\,\,000 + 1\,\,584\,\,000 = 3\,\,312\,\,000\) (đồng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số học sinh của trường THCS đó là \(a\) (học sinh) \(\left( {a \in \mathbb{N},100 \le a < 250} \right)\).
Do khi xếp hàng 10 em thì thừa 8 em nên \(a\) chia 10 dư 8, hay \(\left( {a + 2} \right) \vdots 10\).
Khi xếp hàng 12 em thì thừa 10 em nên \(a\) chia 12 dư 10, hay \(\left( {a + 2} \right) \vdots 12\).
Khi xếp hàng 15 em thì thừa 13 em nên \(a\) chia 15 dư 13, hay \(\left( {a + 2} \right) \vdots 15\).
Từ đó suy ra \(a + 2 \in BC\left( {10,12,15} \right)\).
Ta có: \(10 = 2.5\); \(12 = {2^2}.3\); \(15 = 3.5\).
Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\).
Khi đó \[a + 2 \in BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;240;300;360;...} \right\}\].
Mà \(100 \le a < 250\) nên \(102 \le a + 2 \le 252\), suy ra \(a + 2 \in \left\{ {120;180;240} \right\}\)
Do đó \(a \in \left\{ {118;178;238} \right\}\)
Mặt khác khi số học sinh của trường xếp hàng 17 thì vừa đủ nên \(a \vdots 17\)
Xét 3 trường hợp ở trên ta có \(a = 238\) thỏa mãn.
Vậy trường THCS đó có 238 học sinh.
Lời giải
Với \(x,y\) là số nguyên, từ \(\left( {x + 5} \right)\left( {2y + 1} \right) = 4\), suy ra \(2y + 1\) là ước của 4.
Mà Ư\(\left( 4 \right) = \left\{ {1; - 1;2; - 2;4; - 4} \right\}\).
Do \(y\) là số nguyên nên \(2y + 1\) là số lẻ nên \(2y + 1\) chỉ là ước lẻ của 4.
Khi đó \(2y + 1 \in \left\{ {1; - 1} \right\}\).
Ta có bảng sau:
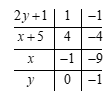
Vậy \[\left( {x;y} \right) \in \left\{ {\left( { - 1;0} \right);\left( { - 9; - 1} \right)} \right\}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(x\) chia hết cho 4;
B. \(x\) chia hết cho 2;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(28;19;0; - 36; - 21\);
B. \( - 49; - 40; - 35; - 20;0\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
