Tổng của hai số 18. Hiệu của hai số là 2. Tìm tỉ số phần trăm của số bé và số lớn.

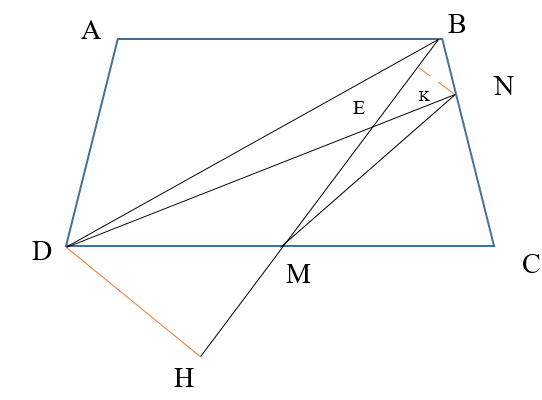
+) Chiều cao của tam giác BDC hạ từ đỉnh B bằng chiều cao của hình thang và bằng 7 m. Suy ra S_BDC = 20 × 7 : 2 = 70 (m²)

+) Tam giác BMC và tam giác BDC có cùng chiều cao hạ từ B xuống DC và đáy MC = \(\frac{1}{2}\) DC nên S_BMC = \(\frac{1}{2}\) S_BDC = \(\frac{1}{2}\) × 70 = 35 (m²)

+) Tam giác BMN và tam giác BMC có cùng chiều cao hạ từ M xuống BC và đáy BN = \(\frac{2}{5}\) BC nên S_BMN = \(\frac{2}{5}\)S_BMC = \(\frac{2}{5}\)× 35 = 14 (m²)

+) Gọi DH là đường cao tam giác MDE và tam giác MBD hạ từ D xuống BM

NK là đường cao tam giác MEN và tam giác MBN hạ từ N xuống MB

+) Vì tam giác MDE và tam giác MEN có chung đáy ME nên \(\frac{{{S_{MDE}}}}{{{S_{MEN}}}} = \frac{{DH}}{{NK}}\)

+) Tam giác DBM và tam giác MNB có chung đáy MB nên \(\frac{{{S_{DBM}}}}{{{S_{MNB}}}} = \frac{{DH}}{{NK}}\)

Suy ra \(\frac{{{S_{MDE}}}}{{{S_{MEN}}}} = \frac{{{S_{DBM}}}}{{{S_{MNB}}}} = \frac{{35}}{{14}} = \frac{5}{2}\)

+) Mặt khác \({S_{MDE}} + {S_{MEN}} = {S_{DMN}} = \frac{1}{2}{S_{DNC}} = \frac{1}{2} \times \frac{3}{5} \times {S_{DBC}} = \frac{1}{2} \times \frac{3}{5} \times 70 = 21\) (m²)

Đưa về bài toán tổng tỉ, suy ra

\({S_{MDE}} = 21:(5 + 2) \times 5 = 15\) (m²)

Đáp số: diện tích tam giác BMN bằng 14 m²

                                             diện tích tam giác DEM bằng 15 m²