Đề thi tuyển sinh vào lớp 6 môn Toán THCS ARCHIMEDES Hà Nội 2025 - 2026 có đáp án
136 người thi tuần này 4.6 412 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi tuyển sinh vào lớp 6 môn Toán THCS Lê Văn Thiêm - TP.Hà Tĩnh 2025 - 2026 có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán Trường CLC Việt Yên - Bắc Giang 2025 - 2026 có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán Trường CLC TP.Hưng Yên 2025 - 2026 có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán THCS Lập Thạch Vĩnh Phúc 2025 - 2026 có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán THCS Lê Quý Đôn, Lý Tự Trọng TP.Lào Cai 2025 - 2026 có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán TP.Thủ Đức - Hồ Chí Minh có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán THCS Trần Mai Ninh - Thanh Hóa 2025 - 2026 có đáp án
Đề thi tuyển sinh vào lớp 6 môn Toán THCS Chất lượng cao - TP.Nam Định 2025 - 2026 có đáp án
Danh sách câu hỏi:
Lời giải
\(A = \frac{3}{{1 \times 2}} - \frac{5}{{2 \times 3}} + \frac{7}{{3 \times 4}} - \frac{9}{{4 \times 5}} + \frac{{11}}{{5 \times 6}} - \frac{{13}}{{6 \times 7}} + \frac{{15}}{{7 \times 8}} - \frac{{17}}{{8 \times 9}} + \frac{{19}}{{9 \times 10}}\)
\(A = \frac{{1 + 2}}{{1 \times 2}} - \frac{{2 + 3}}{{2 \times 3}} + \frac{{3 + 4}}{{3 \times 4}} - \frac{{4 + 5}}{{4 \times 5}} + \frac{{5 + 6}}{{5 \times 6}} - \frac{{6 + 7}}{{6 \times 7}} + \frac{{7 + 8}}{{7 \times 8}} - \frac{{8 + 9}}{{8 \times 9}} + \frac{{9 + 10}}{{9 \times 10}}\)
\(A = \left( {1 + \frac{1}{2}} \right) - \left( {\frac{1}{2} + \frac{1}{3}} \right) + \left( {\frac{1}{3} + \frac{1}{4}} \right) - \left( {\frac{1}{4} + \frac{1}{5}} \right) + \left( {\frac{1}{5} + \frac{1}{6}} \right) - \left( {\frac{1}{6} + \frac{1}{7}} \right) + \left( {\frac{1}{7} + \frac{1}{8}} \right) - \left( {\frac{1}{8} + \frac{1}{9}} \right) + \left( {\frac{1}{9} + \frac{1}{{10}}} \right)\)
\(A = 1 + \frac{1}{{10}}\)
\(A = \frac{{11}}{{10}}\)
Lời giải
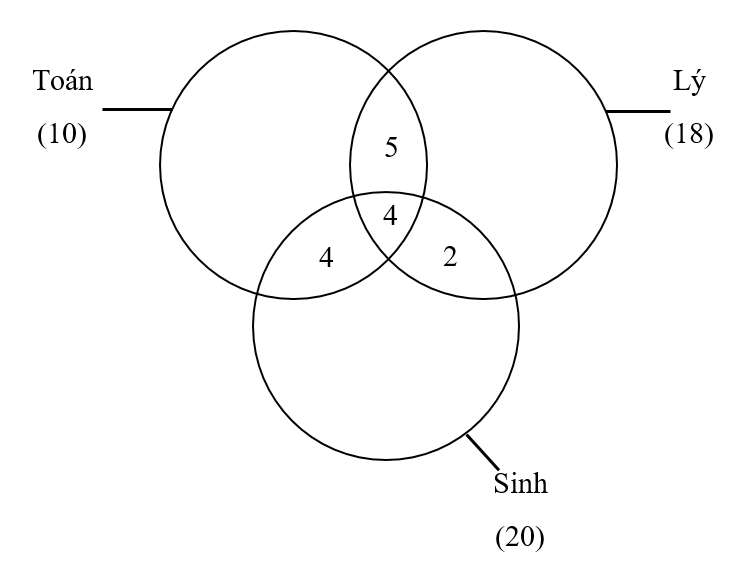
Số bạn giỏi cả 3 môn là: (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Toán và Lý là: 9 – 4 = 5 (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Lý và Sinh là: 6 – 4 = 2 (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Sinh và Toán là: 8 – 4 = 4 (bạn)
Số bạn chỉ giỏi 1 môn là:
(16 – 5 – 4 – 4 ) + (18 – 5 – 4 – 2) + (20 – 4 – 4 – 2) = 20 (bạn)
Đáp số: 20 bạn.
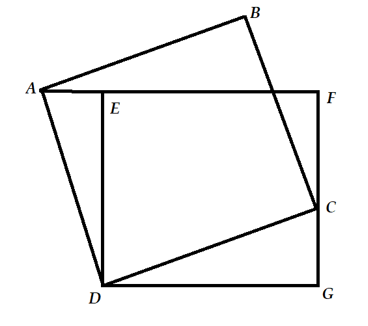
Lời giải
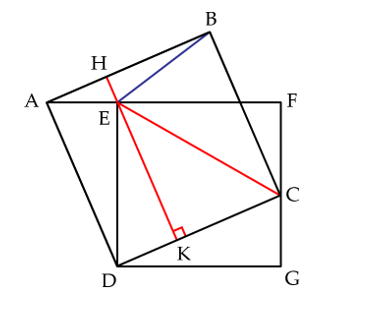
Nối E với C và B với E.
Từ E kẻ đường thẳng vuông góc với DC, cắt AB tại H và cắt DC tại K.
\({S_{DEC}} = \frac{1}{2}{S_{DEFG}} = \frac{1}{2} \times 32 = 16\left( {c{m^2}} \right)\)
\({S_{ABE}} + {S_{DEC}} = \frac{1}{2} \times EH \times AB + \frac{1}{2}EK \times CD\)
\( = \frac{1}{2} \times \left( {EH + EK} \right) \times CD\)
\( = \frac{1}{2} \times {S_{ABCD}}\)
Suy ra \({S_{ABCD}} = \left( {16 + 13} \right) \times 2 = 58\left( {c{m^2}} \right)\)
Lời giải
Ta có: 7 = 7 = 1 + 6 = 2 + 5 = 3 + 4
= 1 + 2 + 4.
Trường hợp 1: 7 số 7 ta có 1 số là 7777777
Trường hợp 2: 1 số 1 và 6 số 6 ta có 7 số: 1666666; 6166666; 6616666;…; 6666661.
Trường hợp 3: Có 2 số 2; 5 số 5.
Xếp số 2 đầu tiên vào 7 vị trí có 7 cách xếp nên khi xếp số 2 còn lại có 6 cách xếp. Vì khi đổi thứ tự 2 số 2 thì không tạo ra số mới nên mỗi cách xếp lặp lại 2 lần, ví dụ 212255555 Và 2221 55555. Ta lập được số số là: (7 × 6) : 2 = 21 (số)
Trường hợp 4: Có 3 số 3; 4 số 4.
Xếp số 3 đầu tiên có 7 cách xếp, số 3 tiếp theo có 6 cách xếp và số 3 còn lại có 5 cách xếp. Vì khi đổi thứ tự 3 số 3 thì không tạo ra số mới nên mỗi cách sắp xếp sẽ lặp lại 6 lần, ví dụ 3132334444; 3133324444;....
Ta lập được số số là: (7 × 6 × 5) : 6 = 35 (số)
Trường hợp 5: Có 1 số 1; 2 số 2; 4 số 4
Xếp số 1 đầu tiên có 7 vị trí nên có 7 cách xếp.
Sau khi xếp số 1 còn lại 6 vị trí thì tương tự 2 số 2 tiếp theo có số cách xếp vào 6 vị trí là: 6 × 5 : 2 = 15 (cách xếp)
Ta lập được số số là: 7 × 15 = 105 (số)
Ta có: 1 + 7 + 21 + 35 + 105 = 169 (số)
Đáp số: 169 mã số.
Lời giải
T =1 × 3 × 5 × ... × 2025 = \(\overline {...5} \) (Vì số lẻ nhân với số co tận cùng là 5 thì tích có chữ số tận cùng là 5)
H = 2 × 2 × 2 × 2 ... × 2 (Có 2025 thừa số 2)
Ta có 2 × 2 × 2 × 2 = 16, nhóm 4 thừa số 2 thì ta có số nhóm là 2025 : 4 = 506 (dư 1).
H = (2 × 2 × 2 × 2) × … × (2 × 2 × 2 × 2)
H = 16 × ... × 16 × 2
H = \(\overline {...6} \) × 2
H = \(\overline {...2} \)
T + H = \(\overline {...5} + \overline {...2} = \overline {...7} \)
Vậy chữ số tận cùng của T + H là chữ số 7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.