Có tồn tại 5 số tự nhiên phân biệt sao cho tổng của từng nhóm ba số bất kỳ là các số tự nhiên liên tiếp hay không?
Có tồn tại 5 số tự nhiên phân biệt sao cho tổng của từng nhóm ba số bất kỳ là các số tự nhiên liên tiếp hay không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta thấy khi ghép nhóm 3 số để tính tổng thì chính là bỏ đi 2 số.
Số cách bỏ đi 2 số là: 5 × 4 : 2 = 10 cách, tức là chúng ta có 10 nhóm 3 số.
Khi nhóm 3 số ta thấy mỗi số sẽ xuất hiện trong 6 nhóm.
(Giải thích: Giả sử 5 số là A, B, C, D, E thì A xuất hiện ở (A, B, C), (A, B, D), (A, B, E), (A, C, D), (A, C, E), (A, D, E) → 6 nhóm)
(Hoặc: có 10 nhóm, mỗi nhóm 3 số → có 10 × 3 = 30 lượt xuất hiện → mỗi số xuất hiện 30 : 5 = 6 lần)
Ta thấy khi tính tổng 3 số ở mỗi nhóm, ta được 10 tổng → mỗi số xuất hiện 6 lần nên khi tính tổng 10 tổng này ta được 1 số chẵn (vì mỗi số xuất hiện 6 lần)
Mà nếu 10 tổng này thành 10 số liên tiếp thì tổng 10 số sẽ có tận cùng là chữ số tận cùng của 0 + 1 + 2 + … + 9 = …5, vô lý.
Vậy không tồn tại 5 số thỏa mãn đề bài.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
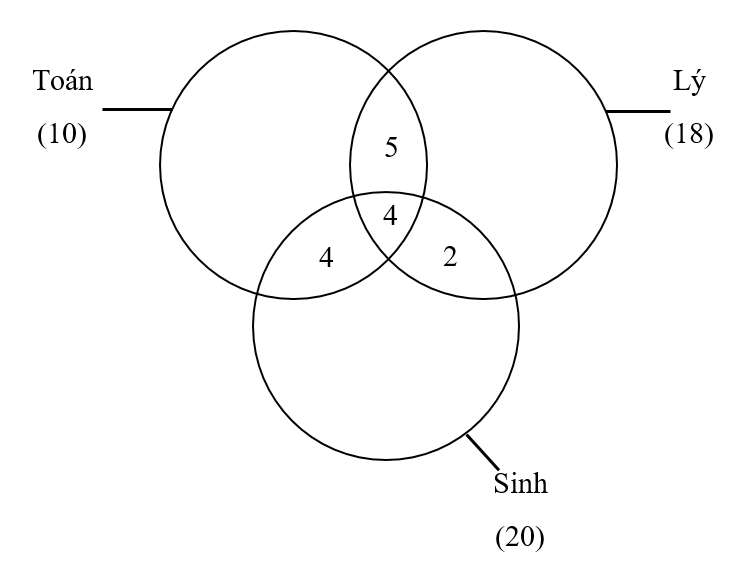
Số bạn giỏi cả 3 môn là: (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Toán và Lý là: 9 – 4 = 5 (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Lý và Sinh là: 6 – 4 = 2 (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Sinh và Toán là: 8 – 4 = 4 (bạn)
Số bạn chỉ giỏi 1 môn là:
(16 – 5 – 4 – 4 ) + (18 – 5 – 4 – 2) + (20 – 4 – 4 – 2) = 20 (bạn)
Đáp số: 20 bạn.
Lời giải
T =1 × 3 × 5 × ... × 2025 = \(\overline {...5} \) (Vì số lẻ nhân với số co tận cùng là 5 thì tích có chữ số tận cùng là 5)
H = 2 × 2 × 2 × 2 ... × 2 (Có 2025 thừa số 2)
Ta có 2 × 2 × 2 × 2 = 16, nhóm 4 thừa số 2 thì ta có số nhóm là 2025 : 4 = 506 (dư 1).
H = (2 × 2 × 2 × 2) × … × (2 × 2 × 2 × 2)
H = 16 × ... × 16 × 2
H = \(\overline {...6} \) × 2
H = \(\overline {...2} \)
T + H = \(\overline {...5} + \overline {...2} = \overline {...7} \)
Vậy chữ số tận cùng của T + H là chữ số 7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập