Lớp 6C1 có 16 học sinh giỏi Toán, 15 học sinh giỏi Lý và 11 học sinh giỏi Sinh. Có 9 bạn giỏi Toán và Lý, có 6 bạn giỏi Lý và Sinh, có 8 bạn giỏi Sinh và Toán. Có đúng 11bạn giỏi đúng hai môn. Hỏi có bao nhiêu bạn chỉ giỏi một trong ba môn đã cho?
Lớp 6C1 có 16 học sinh giỏi Toán, 15 học sinh giỏi Lý và 11 học sinh giỏi Sinh. Có 9 bạn giỏi Toán và Lý, có 6 bạn giỏi Lý và Sinh, có 8 bạn giỏi Sinh và Toán. Có đúng 11bạn giỏi đúng hai môn. Hỏi có bao nhiêu bạn chỉ giỏi một trong ba môn đã cho?
Quảng cáo
Trả lời:
Giải bởi Vietjack
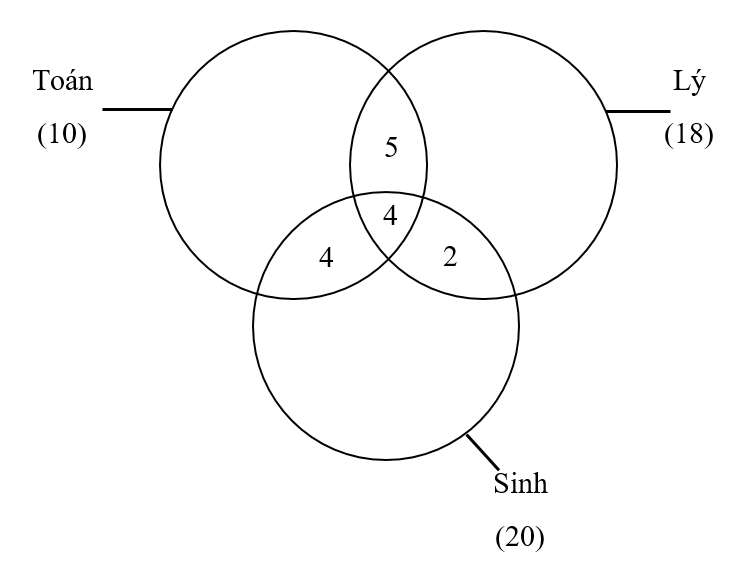
Số bạn giỏi cả 3 môn là: (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Toán và Lý là: 9 – 4 = 5 (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Lý và Sinh là: 6 – 4 = 2 (bạn)
Từ đó tính được các bạn chỉ giỏi 2 môn Sinh và Toán là: 8 – 4 = 4 (bạn)
Số bạn chỉ giỏi 1 môn là:
(16 – 5 – 4 – 4 ) + (18 – 5 – 4 – 2) + (20 – 4 – 4 – 2) = 20 (bạn)
Đáp số: 20 bạn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Có 100 – 90 = 10 bạn không làm đúng bài 1. (1)
Có 100 – 85 = 15 bạn không làm đúng bài 2. (2)
Có 100 – 80 = 20 bạn không làm đúng bài 3. (3)
Có 100 – 75 = 25 bạn không làm đúng bài 4. (4)
Để ít nhất các bạn làm đúng cả 4 bài thì cần nhiều nhất các bạn không làm đúng cả 4 bài.
Khi đó các bạn nhắc đến ở (1), (2), (3) và (4) ở trên là không trùng nhau, tức là có nhiều
nhất 10 + 15 + 20 + 25 = 70 bạn không giỏi cả 4 môn, tức là có ít nhất 100 – 70 = 30 bạn giỏi cả 4 môn.
Đáp số: 30 bạn.
Lời giải
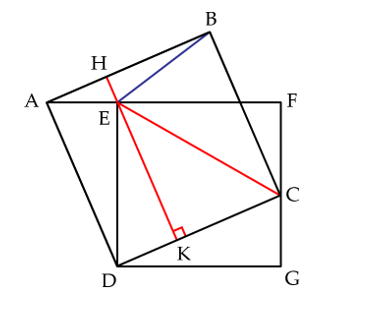
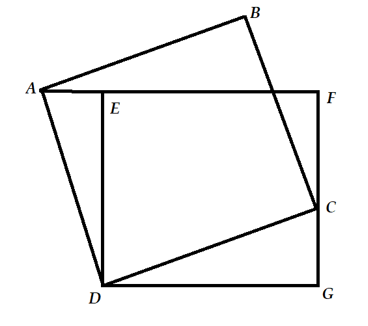
Nối E với C và B với E.
Từ E kẻ đường thẳng vuông góc với DC, cắt AB tại H và cắt DC tại K.
\({S_{DEC}} = \frac{1}{2}{S_{DEFG}} = \frac{1}{2} \times 32 = 16\left( {c{m^2}} \right)\)
\({S_{ABE}} + {S_{DEC}} = \frac{1}{2} \times EH \times AB + \frac{1}{2}EK \times CD\)
\( = \frac{1}{2} \times \left( {EH + EK} \right) \times CD\)
\( = \frac{1}{2} \times {S_{ABCD}}\)
Suy ra \({S_{ABCD}} = \left( {16 + 13} \right) \times 2 = 58\left( {c{m^2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập