Một hộp có 20 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \[1\,;\,\,2\,;\,\,3\,;\,\,...\,;\,\,19\,;\,\,20.\] Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) A: "Số xuất hiện trên thẻ nhỏ hơn 25".
b) B: "Số xuất hiện trên thẻ là số thập phân".
e) E: "Số xuất hiện trên thẻ là số lẻ".
c) C: "Số xuất hiện trên thẻ nhỏ hơn 20 ".
f) F: "Số xuất hiện trên thẻ là số chia hết cho 4".
d) D: "Số xuất hiện trên thẻ lớn hơn 17 ".
g) G: "Số xuất hiện trên thẻ là số nguyên tố".
h) H: "Số xuất hiện trên thẻ là số chia cho 3 dư 2".
Một hộp có 20 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \[1\,;\,\,2\,;\,\,3\,;\,\,...\,;\,\,19\,;\,\,20.\] Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) A: "Số xuất hiện trên thẻ nhỏ hơn 25".
b) B: "Số xuất hiện trên thẻ là số thập phân".
e) E: "Số xuất hiện trên thẻ là số lẻ".
c) C: "Số xuất hiện trên thẻ nhỏ hơn 20 ".
f) F: "Số xuất hiện trên thẻ là số chia hết cho 4".
d) D: "Số xuất hiện trên thẻ lớn hơn 17 ".
g) G: "Số xuất hiện trên thẻ là số nguyên tố".
h) H: "Số xuất hiện trên thẻ là số chia cho 3 dư 2".
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Tất cả các thẻ trong hộp đều ghi số nhỏ nhỏ hơn 25.
Do đó, xác suất của biến cố A là \[100\% \].
b) Tất cả các thẻ trong hộp đều ghi số tự nhiên hay không có thẻ nào ghi số thập phân.
Do đó, xác suất của biến cố B là \[0\% \].
c) Trong 20 thẻ trong hộp thì có 19 thẻ ghi số nhỏ hơn 20 gồm \[\left\{ {1\,;\,\,2\,;\,\,3\,;\,\,...\,;\,\,19} \right\}.\]
Do đó, xác suất của biến cố C là \[\frac{{19}}{{20}}\].
d) Trong 20 thẻ trong hộp thì có 3 thẻ ghi số lớn hơn 17 gồm \[\left\{ {18\,;\,\,19\,;\,\,20} \right\}.\]
Do đó, xác suất của biến cố D là \[\frac{3}{{20}}\].
e) Trong 20 thẻ trong hộp thì có 10 thẻ ghi số chẵn và 10 thẻ ghi số lẻ.
Do đó, xác suất của biến cố E là \[50\% \].
g) Trong 20 thẻ trong hộp có các số chia hết cho 4 là \[4\,;\,\,8\,;\,\,12\,;\,\,16\,;\,\,20\].
Xác suất số chia hết cho 4 là \[\frac{5}{{20}}\].
h) Các số nguyên tố trên thẻ là \[2\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,13\,;\,\,17\,;\,\,19\];
Xác suất xuất hiện số nguyên tố là \[\frac{7}{{20}}\];
i) Các số chia 3 dư 2 là \[2\,;\,\,5\,;\,\,8\,;\,\,11\,;\,\,14\,;\,\,17\,;\,\,20\];
Xác suất xuất hiện là \[\frac{7}{{20}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Bảng thống kê cân nặng của 30 bạn học sinh lớp 7A như sau:
|
Cân nặng (kg) |
39 |
41 |
42 |
45 |
|
Số học sinh |
3 |
6 |
12 |
9 |
b) Biểu đồ đoạn thẳng biểu diễn dữ liệu trên là
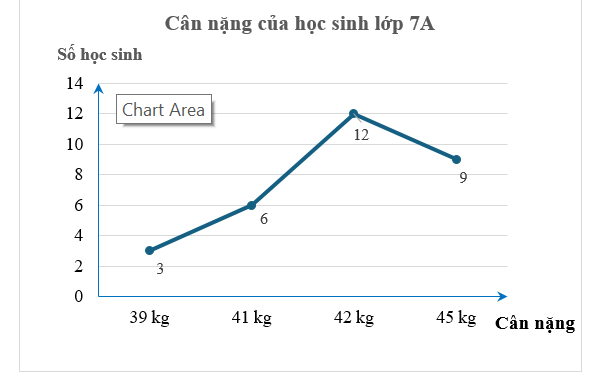
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập