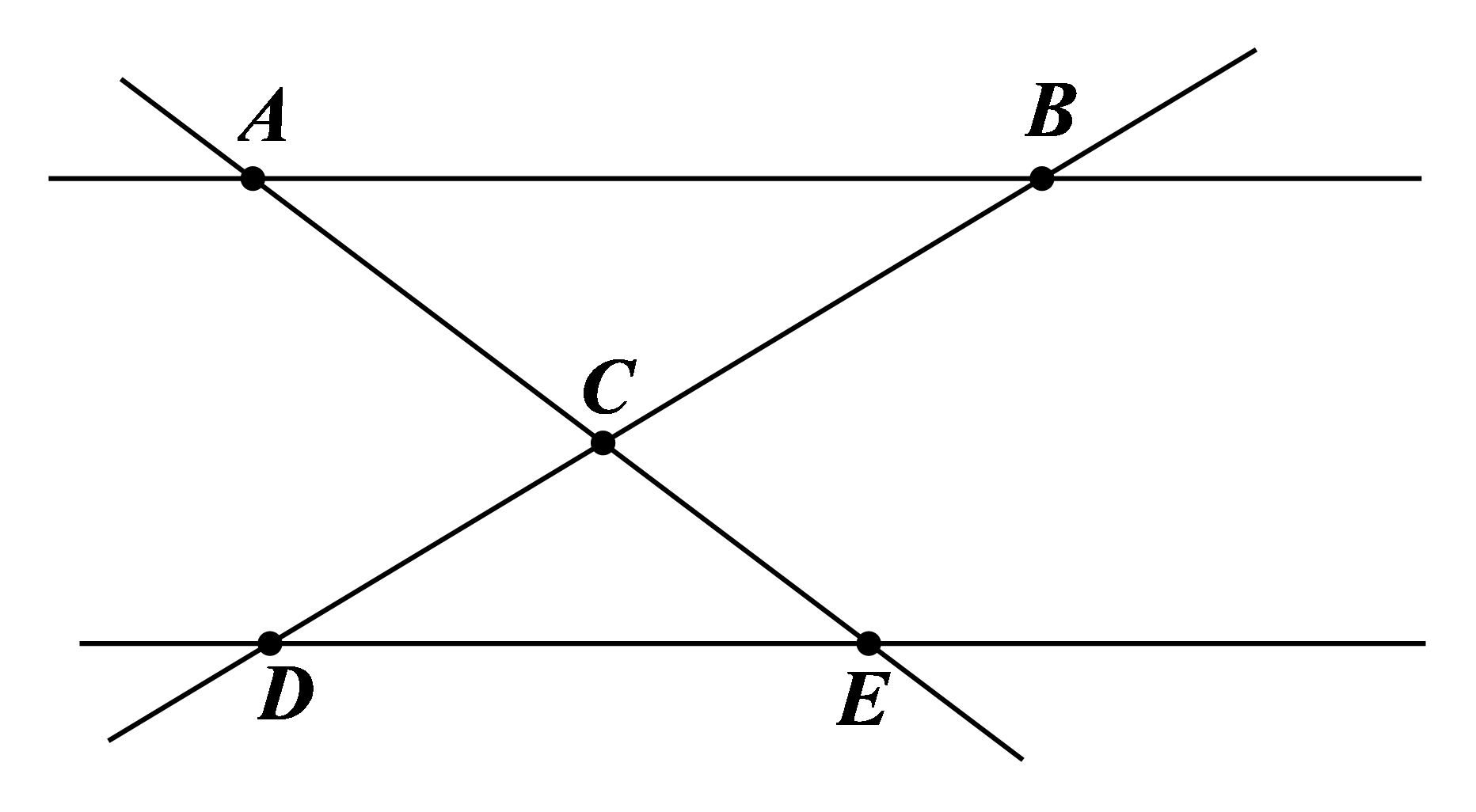Hai vòi nước cùng chảy vào một cái bể không có nước. Trong một giờ, vòi thứ nhất chảy vào được \(\frac{1}{3}\) bể, vòi thứ hai chảy vào được \(\frac{2}{5}\) bể. Hỏi vòi nào chảy nhanh hơn và trong một giờ, cả hai vòi chảy được bao nhiêu phần bể?
Hai vòi nước cùng chảy vào một cái bể không có nước. Trong một giờ, vòi thứ nhất chảy vào được \(\frac{1}{3}\) bể, vòi thứ hai chảy vào được \(\frac{2}{5}\) bể. Hỏi vòi nào chảy nhanh hơn và trong một giờ, cả hai vòi chảy được bao nhiêu phần bể?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Ta có: \(\frac{1}{3} = \frac{5}{{15}}\) và \(\frac{2}{5} = \frac{6}{{15}}.\)
Do \(\frac{5}{{15}} < \frac{6}{{15}}\) nên \(\frac{1}{3} < \frac{2}{5}.\) Vì vậy, vòi thứ hai chảy nhanh hơn vòi thứ nhất.
Trong một giờ, cả hai vòi chảy được số phần bể là: \(\frac{1}{3} + \frac{2}{5} = \frac{5}{{15}} + \frac{6}{{15}} = \frac{{11}}{{15}}\) (bể).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Chỉ với hai lần cưa, người nông dân cần cưa thanh vàng thành ba phần: \(\frac{1}{7}\), \(\frac{2}{7}\) và \(\frac{4}{7}\).
Và khi đó, người nông dân sẽ trả lương mỗi ngày cho thợ như sau:
Thứ hai: Trả \(\frac{1}{7}\) thanh vàng.
Thứ ba: Trả \(\frac{2}{7}\) thanh vàng và lấy lại \(\frac{1}{7}\) thanh vàng.
Thứ tư: Đưa lại \(\frac{1}{7}\) thanh vàng cho người thợ.
Thứ năm: Đưa lại \(\frac{4}{7}\) thanh vàng và lấy lại \(\frac{1}{7}\) và \(\frac{2}{7}\) thanh vàng.
Thứ sáu: Đưa \(\frac{1}{7}\) thanh vàng.
Thứ bảy: Đưa \(\frac{2}{7}\) thanh vàng và lấy lại \(\frac{1}{7}\) thanh vàng từ thợ.
Chủ nhật: Trả nội \(\frac{1}{7}\) thanh vàng còn lại.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải:
Ta có \[\frac{{2025}}{1} = 2025 = \underbrace {1 + 1 + 1... + 1}_{2025\,\,so\,\,hang}\]
Khi đó:
\(B = \frac{{2025}}{1} + \frac{{2024}}{2} + \frac{{2013}}{3} + \ldots + \frac{1}{{2025}}\)
\( = 1 + \left( {\frac{{2024}}{2} + 1} \right) + \left( {\frac{{2013}}{3} + 1} \right) + \ldots + \left( {\frac{1}{{2025}} + 1} \right)\)
\( = 1 + \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}}\)
\( = \frac{{2026}}{2} + \frac{{2026}}{3} + ... + \frac{{2026}}{{2025}} + \frac{{2026}}{{2026}}\)
\(B = 2026 \cdot \left( {\frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{2025}} + \frac{1}{{2026}}} \right) = 2026A\)
Ta có \(\frac{B}{A} = \frac{{2026A}}{A} = 2026.\)
Vậy \(\frac{B}{A} = 2026.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập