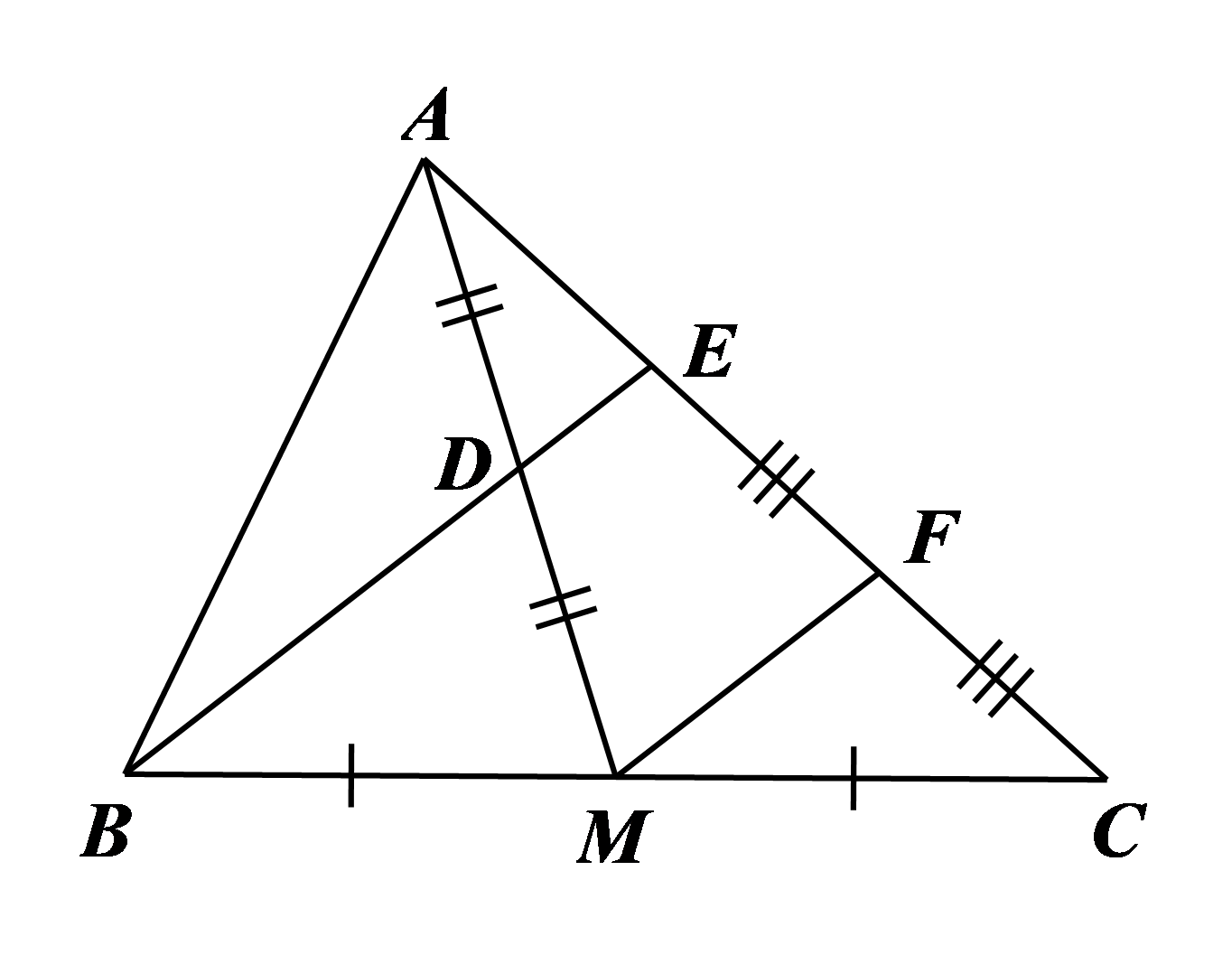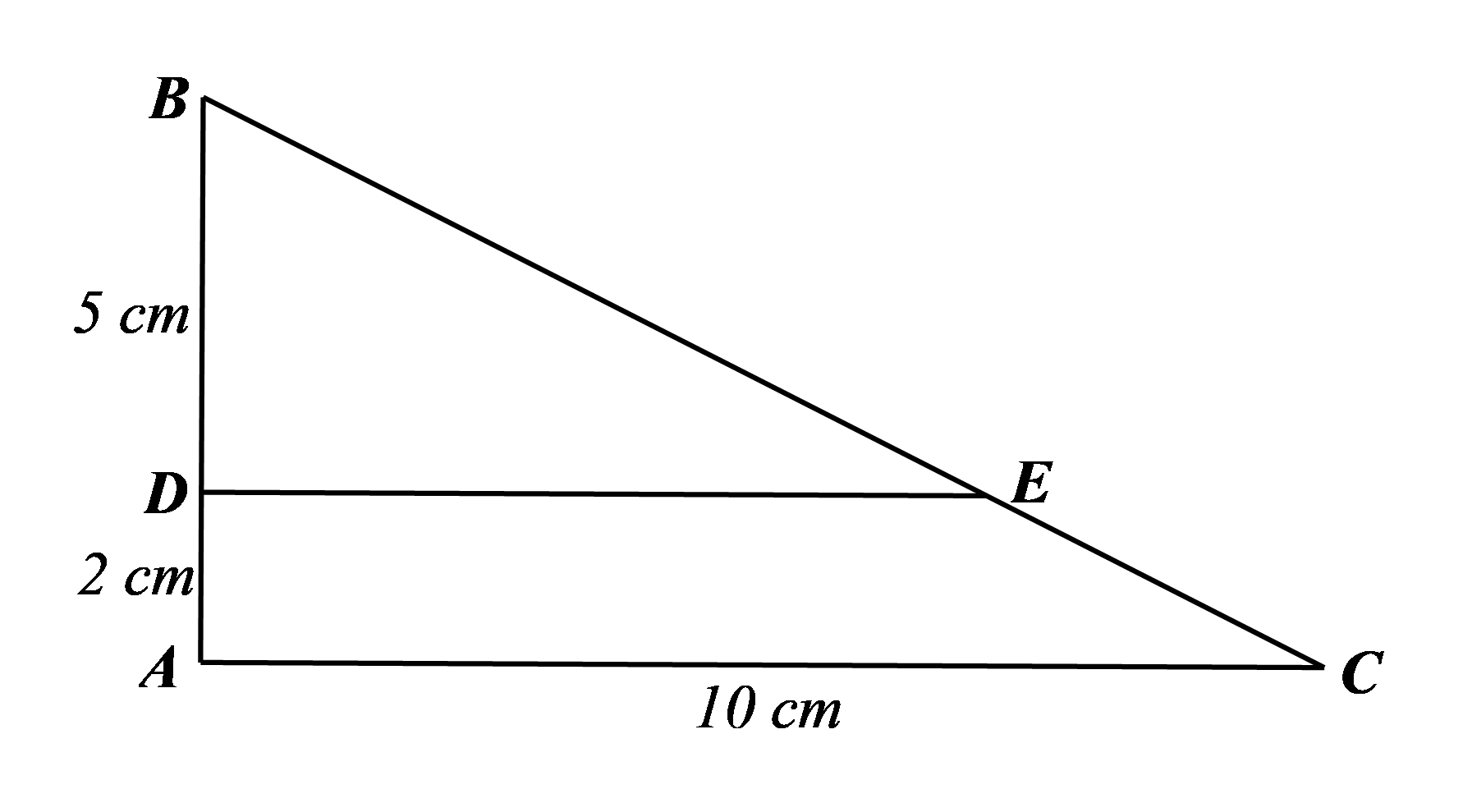Cho tam giác \(ABC,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AM,\,\,E\) là giao điểm của \(BD\) và \(AC,\) \(F\) là trung điểm của \(EC.\) Biết \(AC = 9{\rm{\;cm}},\) độ dài đoạn \(AE\) là
A. \(4,5{\rm{\;cm}}.\)
B. \(3{\rm{\;cm}}.\)
C. \(2{\rm{\;cm}}.\)
D. \(6{\rm{\;cm}}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Hướng dẫn giải Đáp án đúng là: B Xét \[\Delta BCE\] có \(M,\,\,F\) lần lượt là trung điểm của \(BC,\,\,EC\) nên \(MF\) là đường trung bình của tam giác, do đó \(MF\,{\rm{//}}\,BE,\) hay \(MF\,{\rm{//}}\,DE.\) |
|
Xét \(\Delta AMF\) có \(D\) là trung điểm của \(AM\) và \(DE\,{\rm{//}}\,MF\) nên \(DE\) là đường trung bình của tam giác, do đó \(E\) là trung điểm của \(AF.\) Suy ra \(AE = EF.\)
Mà \(F\) là trung điểm của \(EC\) nên \(EF = FC,\) do đó \(AE = EF = FC\) hay \(AE = \frac{1}{3}AC = \frac{1}{3} \cdot 9 = 3{\rm{\;cm}}.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\frac{3}{{10}}\].
B. \[\frac{1}{2}\].
C. \[\frac{2}{5}\].
D. \[\frac{1}{5}\].
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Dũng ra búa tất cả 4 lần trong 10 ván chơi nên xác suất thực nghiệm của sự kiện “Dũng ra búa” là \(\frac{4}{{10}} = \frac{2}{5}.\)
Câu 2
A. \(\frac{4}{{13}}.\)
B. \(\frac{5}{{13}}.\)
C. \(\frac{8}{{13}}.\)
D. \(\frac{1}{{13}}.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Tổ Cường có 3 bạn nam và 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là \(\frac{{3 + 1}}{{13}} = \frac{4}{{13}}.\)
Câu 3
A. \(16{\rm{\;cm}}\) và \(12{\rm{\;cm}}{\rm{.}}\)
B. \(14{\rm{\;cm}}\) và \(14{\rm{\;cm}}{\rm{.}}\)
C. \(14,3{\rm{\;cm}}\) và \(10,7{\rm{\;cm}}{\rm{.}}\)
D. \(12{\rm{\;cm}}\) và \(16{\rm{\;cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}.\)
B. \(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}.\)
C. \[\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}.\]
D. \(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(x = 4,2{\rm{\;cm}}{\rm{.}}\)
B. \[x = 2,5{\rm{\;cm}}{\rm{.}}\]
C. \(x = 7{\rm{\;cm}}{\rm{.}}\)
D. \(x = 5,25{\rm{\;cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(20\% .\)
B. \(30\% .\)
C. \(15\% .\)
D. \(40\% .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập