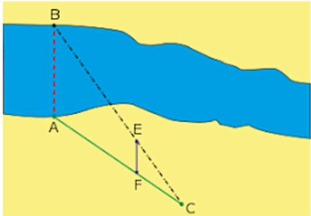
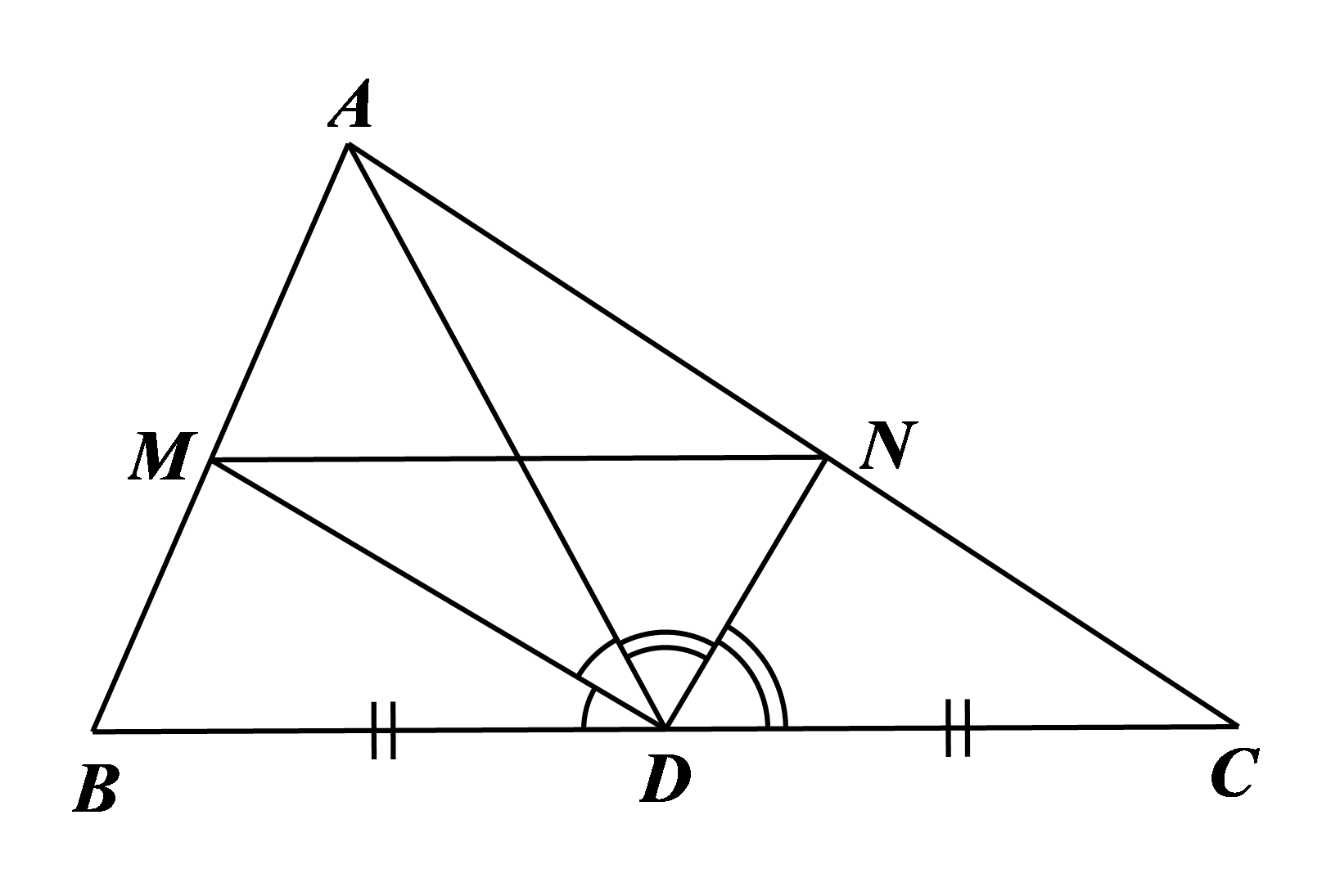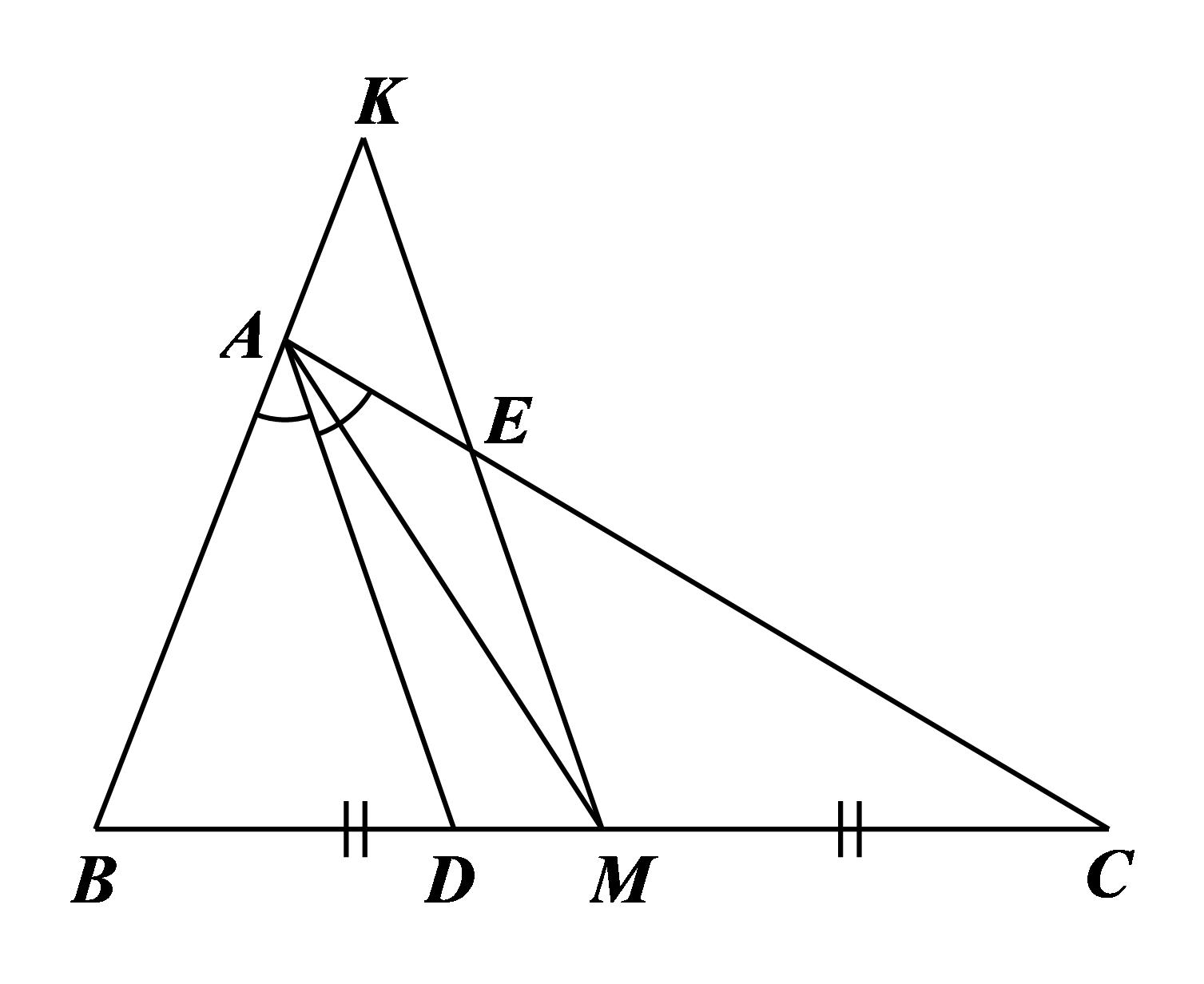Để đo khoảng cách giữa hai vị trí \[B\] và \[E\] ở hai bên bờ sông, bác Minh chọn ba vị trí \[A,{\rm{ }}F,{\rm{ }}C\] cùng nằm ở bên bờ sông sao cho ba điểm \[C,{\rm{ }}E,{\rm{ }}B\]thẳng hàng; ba điểm \[C,{\rm{ }}F,{\rm{ }}A\] thẳng hàng và \[AB{\rm{ }}\,{\rm{//}}\,EF.\] Sau đó bác Minh đo được \[AF = 50{\rm{ \;m}},\] \[FC = 35{\rm{\;m}}\] và \[EC = 42{\rm{\;m}}.\] Tính khoảng cách giữa hai vị trí \[B\] và \[E.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét \(\Delta ABC\) có \[AB{\rm{ }}\,{\rm{//}}\,EF,\] theo định lí Thalès ta có \(\frac{{EC}}{{EB}} = \frac{{CF}}{{FA}},\) hay \(\frac{{42}}{{BE}} = \frac{{35}}{{50}}.\)
Suy ra \(BE = \frac{{42 \cdot 50}}{{35}} = 60{\rm{\;m}}{\rm{.}}\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Xét \(\Delta ABD\) có \(DM\) là đường phân giác của \[\widehat {ADB}\] nên \[\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\] (tính chất đường phân giác trong tam giác). b) Xét \(\Delta ACD\) có \(DN\) là đường phân giác của \[\widehat {ADC}\] nên \[\frac{{DA}}{{DC}} = \frac{{NA}}{{NC}}\] (tính chất đường phân giác trong tam giác). |
|
Mà \[\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\] (câu a) và \[DB = DC\] nên \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}.\]
c) Xét \(\Delta ABC\) có: \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}\] (câu b) nên \[MN\,{\rm{//}}\,BC\](định lí Thalès đảo).
Lời giải
|
a) Vì \(AD\,{\rm{//}}\,KM\) nên \(\widehat {BAD} = \widehat {BKM}\) (đồng vị). Vì \(AD\,{\rm{//}}\,EM\) nên \(\widehat {CAD} = \widehat {CEM}\) (đồng vị). Mà \(AD\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAD} = \widehat {CAD}.\) Do đó \(\widehat {BKM} = \widehat {CEM},\) lại có \(\widehat {CEM} = \widehat {AEK}\) nên \(\widehat {BKM} = \widehat {AEK}\) hay \(\widehat {AKE} = \widehat {AEK}.\) |
|
Tam giác \(AEK\) có \(\widehat {AKE} = \widehat {AEK}\) nên là tam giác cân tại \(A.\)
b) Xét \(\Delta ACD\) có \(EM\,{\rm{//}}\,AD,\) theo định lí Thalès ta có \(\frac{{AE}}{{EC}} = \frac{{DM}}{{MC}}.\)
Mà \(\Delta AEK\) cân tại \(A\) nên \(AK = AE.\)
Lại có điểm \(M\) là trung điểm của \(BC\) nên \(MB = MC.\)
Do đó \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}.\)
c) Xét \(\Delta BMK\) có \(AD\,{\rm{//}}\,KM,\) theo định lí Thalès ta có \(\frac{{DM}}{{BM}} = \frac{{AK}}{{BK}}.\)
Theo câu a, ta có \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}\) nên \(\frac{{AK}}{{EC}} = \frac{{AK}}{{BK}},\) do đó \(EC = BK.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập