Đề cương ôn tập giữa kì 2 Toán 8 Cánh diều cấu trúc mới (Tự luận) có đáp án - Phần 2
18 người thi tuần này 4.6 357 lượt thi 11 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
|
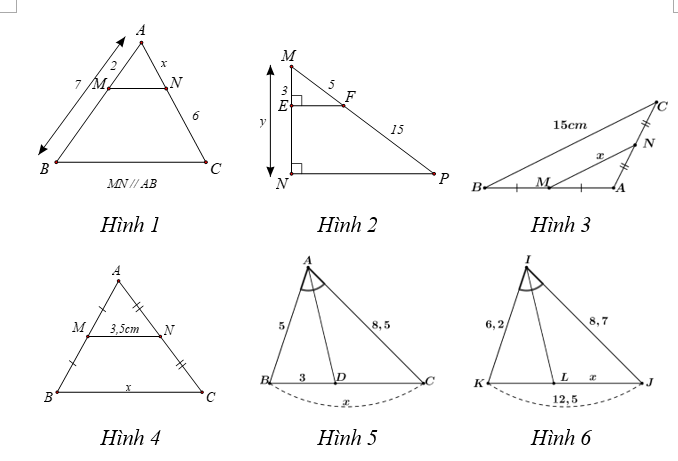
⦁ Hình 1: Ta có \(MB = AB - AM = 7 - 2 = 5.\) Tam giác \(ABC\) có \(MN\,{\rm{//}}\,AB,\) theo định lí Thalès ta có: \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) hay \(\frac{2}{5} = \frac{x}{6},\) suy ra \(x = \frac{{12}}{5}.\) Vậy \(x = \frac{{12}}{5}.\) |
Hình 1 |
|
⦁ Hình 2: Ta có: \[EF \bot MN,\,\,NP \bot MN\] nên \[EF\,{\rm{//}}\,NP.\] \(MP = MF + FP = 5 + 15 = 20.\) Tam giác \[MNP\] có \[EF\,{\rm{//}}\,NP,\] theo định lí Thalès ta có: \[\frac{{ME}}{{MN}} = \frac{{MF}}{{MP}}\] hay \(\frac{3}{y} = \frac{5}{{20}},\) suy ra \(y = \frac{{3 \cdot 20}}{5} = 12.\) Vậy \(y = 12.\) |
Hình 2 |
|
⦁ Hình 3: Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC = \frac{1}{2} \cdot 15 = 7,5\,\,\left( {{\rm{cm}}} \right).\] Vậy \[x = 7,5\,\,{\rm{cm}}.\] |
Hình 3 |
|
⦁ Hình 4: Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC.\] Suy ra \[x = BC = 2MN = 2 \cdot 3,5 = 7\left( {{\rm{cm}}} \right).\] Vậy \(x = 7{\rm{\;cm}}.\) |
Hình 4 |
|
⦁ Hình 5: Xét tam giác \[ABC\] có \[AD\] là phân giác trong góc \[\widehat {BAC}\] (do \[\widehat {BAD} = \widehat {CAD}),\] nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}},\) hay \[\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\] Do đó \[\frac{3}{5} = \frac{{DC}}{{8,5}},\] suy ra \[DC = \frac{{8,5 \cdot 3}}{5} = 5,1.\] Khi đó \(x = BC = DB + DC = 3 + 5,1 = 8,1.\) |
Hình 5 |
|
⦁ Hình 6: Xét tam giác \[IKJ\] có \[IL\] là phân giác trong góc \[\widehat {KIJ}\] (do \(\widehat {KIL} = \widehat {JIL}),\) nên \(\frac{{IK}}{{IJ}} = \frac{{LK}}{{LJ}}\) hay \[\frac{{LK}}{{IK}} = \frac{{LJ}}{{IJ}}\] Theo tính chất dãy tỉ số bằng nhau ta có: \[\frac{{LK}}{{6,2}} = \frac{{LJ}}{{8,7}} = \frac{{LK + LJ}}{{6,2 + 8,7}} = \frac{{KJ}}{{14,9}} = \frac{{12,5}}{{14,9}}.\] Suy ra \[LJ = \frac{{12,5}}{{14,9}} \cdot 8,7 \approx 7,3.\] |
Hình 6 |
Lời giải
Hướng dẫn giải
|
a) Xét \(\Delta ABC\) có \(AB \bot AC;\,\,IN \bot AC\) nên \(AB\,{\rm{//}}\,IN.\) Mà \(I\) là trung điểm của \(BC\) nên \(IN\) là đường trung bình của tam giác, do đó \(N\) là trung điểm của \(AC.\) Xét tứ giác \(ADCI\) có: \(N\) là trung điểm của \(ID,\,\,AC\) nên \(ADCI\) là hình bình hành. |
|
Lại có \(IN \bot AC\) hay \(ID \bot AC\) nên hình bình hành \(ADCI\) là hình thoi.\(\)
|
b) Kẻ \(IH\,{\rm{//}}\,BK\,\,\left( {H \in CD} \right),\) mà \(I\) là trung điểm của \(BC,\) nên \(IH\) là đường trung bình của \(\Delta BKC.\) Do đó \(H\) là trung điểm của \(KC\) hay \(KH = HC\,\,\left( 1 \right)\) Xét \[\Delta DIH\] có \(N\) là trung điểm của \[DI\] và \[NK\,{\rm{//}}\,IH\] (do \[BK\,{\rm{//}}\,IH)\] nên \(NK\) là đường trung bình của \[\Delta DIH,\] suy ra \(K\)là trung điểm của \(DH\) hay \(DK = KH\,\,\left( 2 \right)\) |
|
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(DK = KH = HC.\) Do đó \(\frac{{DK}}{{DC}} = \frac{1}{3}.\)
Lời giải
|
a) Xét \(\Delta ABD\) có \(DM\) là đường phân giác của \[\widehat {ADB}\] nên \[\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\] (tính chất đường phân giác trong tam giác). b) Xét \(\Delta ACD\) có \(DN\) là đường phân giác của \[\widehat {ADC}\] nên \[\frac{{DA}}{{DC}} = \frac{{NA}}{{NC}}\] (tính chất đường phân giác trong tam giác). |
|
Mà \[\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\] (câu a) và \[DB = DC\] nên \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}.\]
c) Xét \(\Delta ABC\) có: \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}\] (câu b) nên \[MN\,{\rm{//}}\,BC\](định lí Thalès đảo).
Lời giải
|
a) Vì \(AD\,{\rm{//}}\,KM\) nên \(\widehat {BAD} = \widehat {BKM}\) (đồng vị). Vì \(AD\,{\rm{//}}\,EM\) nên \(\widehat {CAD} = \widehat {CEM}\) (đồng vị). Mà \(AD\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAD} = \widehat {CAD}.\) Do đó \(\widehat {BKM} = \widehat {CEM},\) lại có \(\widehat {CEM} = \widehat {AEK}\) nên \(\widehat {BKM} = \widehat {AEK}\) hay \(\widehat {AKE} = \widehat {AEK}.\) |
|
Tam giác \(AEK\) có \(\widehat {AKE} = \widehat {AEK}\) nên là tam giác cân tại \(A.\)
b) Xét \(\Delta ACD\) có \(EM\,{\rm{//}}\,AD,\) theo định lí Thalès ta có \(\frac{{AE}}{{EC}} = \frac{{DM}}{{MC}}.\)
Mà \(\Delta AEK\) cân tại \(A\) nên \(AK = AE.\)
Lại có điểm \(M\) là trung điểm của \(BC\) nên \(MB = MC.\)
Do đó \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}.\)
c) Xét \(\Delta BMK\) có \(AD\,{\rm{//}}\,KM,\) theo định lí Thalès ta có \(\frac{{DM}}{{BM}} = \frac{{AK}}{{BK}}.\)
Theo câu a, ta có \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}\) nên \(\frac{{AK}}{{EC}} = \frac{{AK}}{{BK}},\) do đó \(EC = BK.\)
Lời giải
|
a) Xét \(\Delta ADC\) có \(E,\,\,I\) lần lượt là trung điểm của \(AD,\,\,AC\) nên \[EI\] là đường trung bình của \(\Delta ADC.\) Do đó \(EI\,{\rm{//}}\,CD\) và \(EI = \frac{{C{\rm{D}}}}{2}.\) Xét \(\Delta ABC\) có \(I,\,\,F\) lần lượt là trung điểm của \(AC,\,\,BC\) nên \[IF\] là đường trung bình của \(\Delta ABC.\) Do đó \(IF\,{\rm{//}}\,AB\) và \(IF = \frac{{AB}}{2}.\) |
|
b) Trong \(\Delta EIF\) ta có: \(EF \le EI + IF\) (dấu "=" xảy ra khi \[E,\,\,I,\,\,F\] thẳng hàng)
Mà \(EI = \frac{{C{\rm{D}}}}{2};\,\,IF = \frac{{AB}}{2}\) (chứng minh ở câu a)
Do đó \[EF \le \frac{{AB + CD}}{2}.\]
Vậy \[EF \le \frac{{AB + CD}}{2}\] (dấu bằng xảy ra khi \(AB\,{\rm{//}}\,CD).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
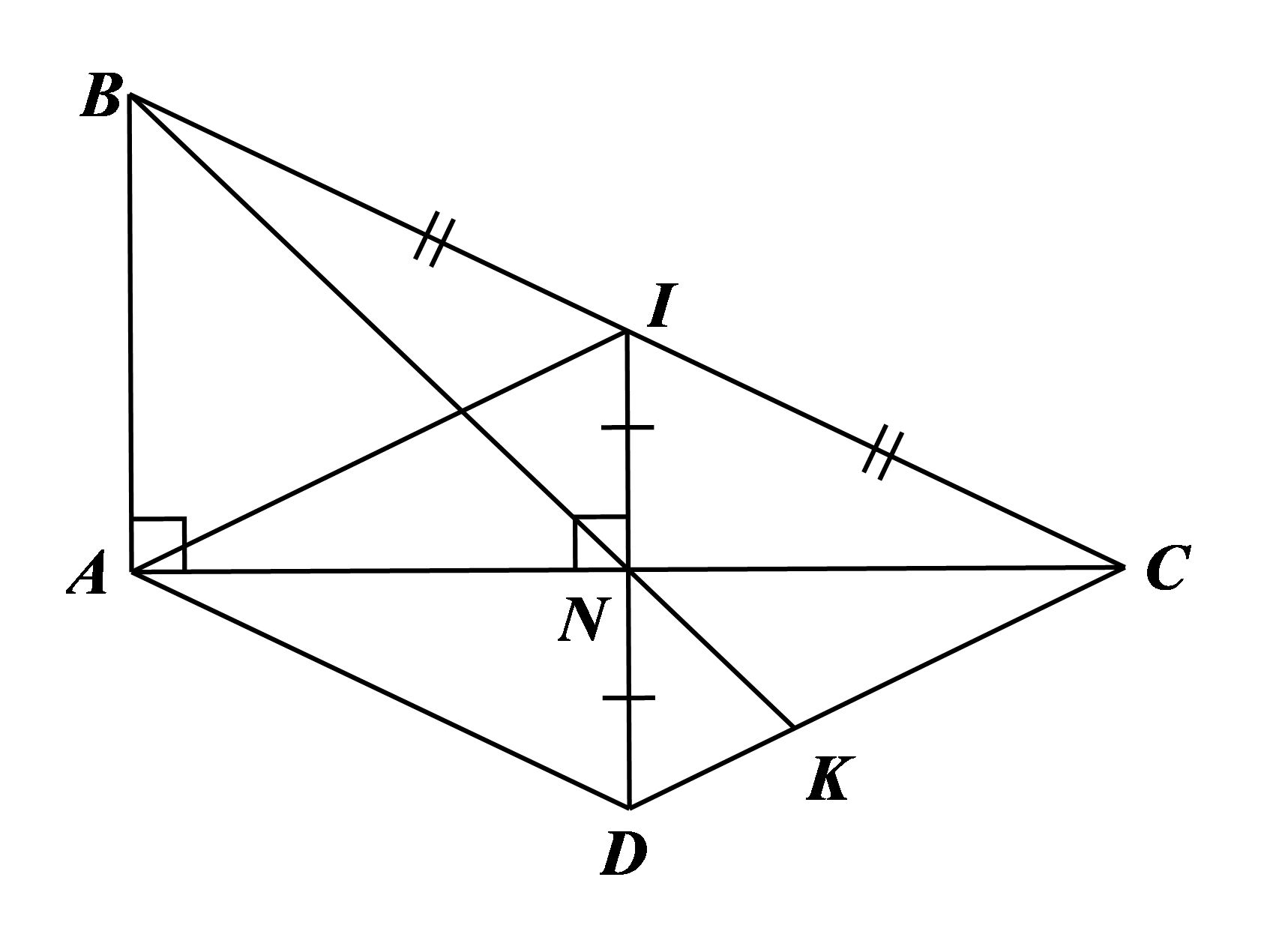
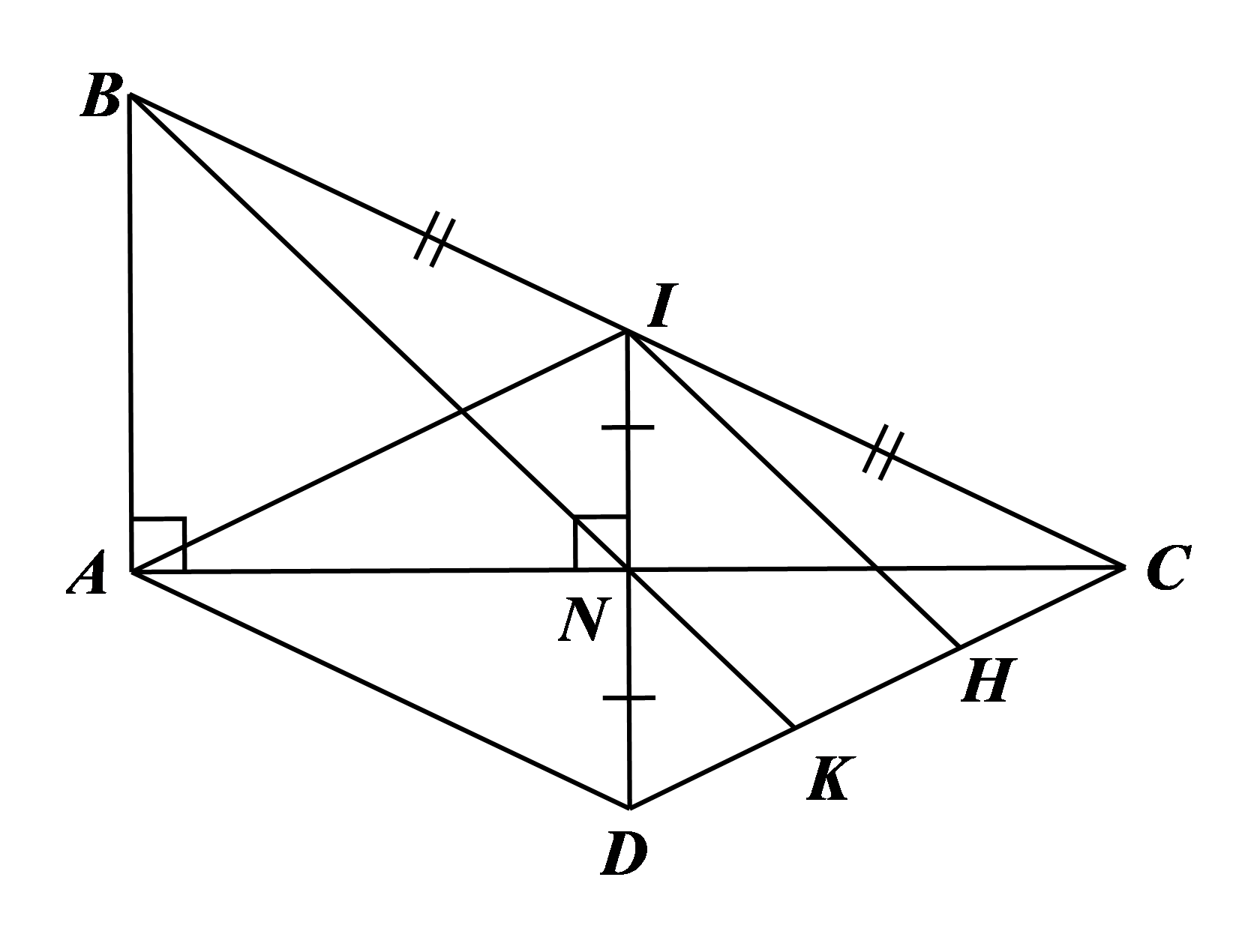
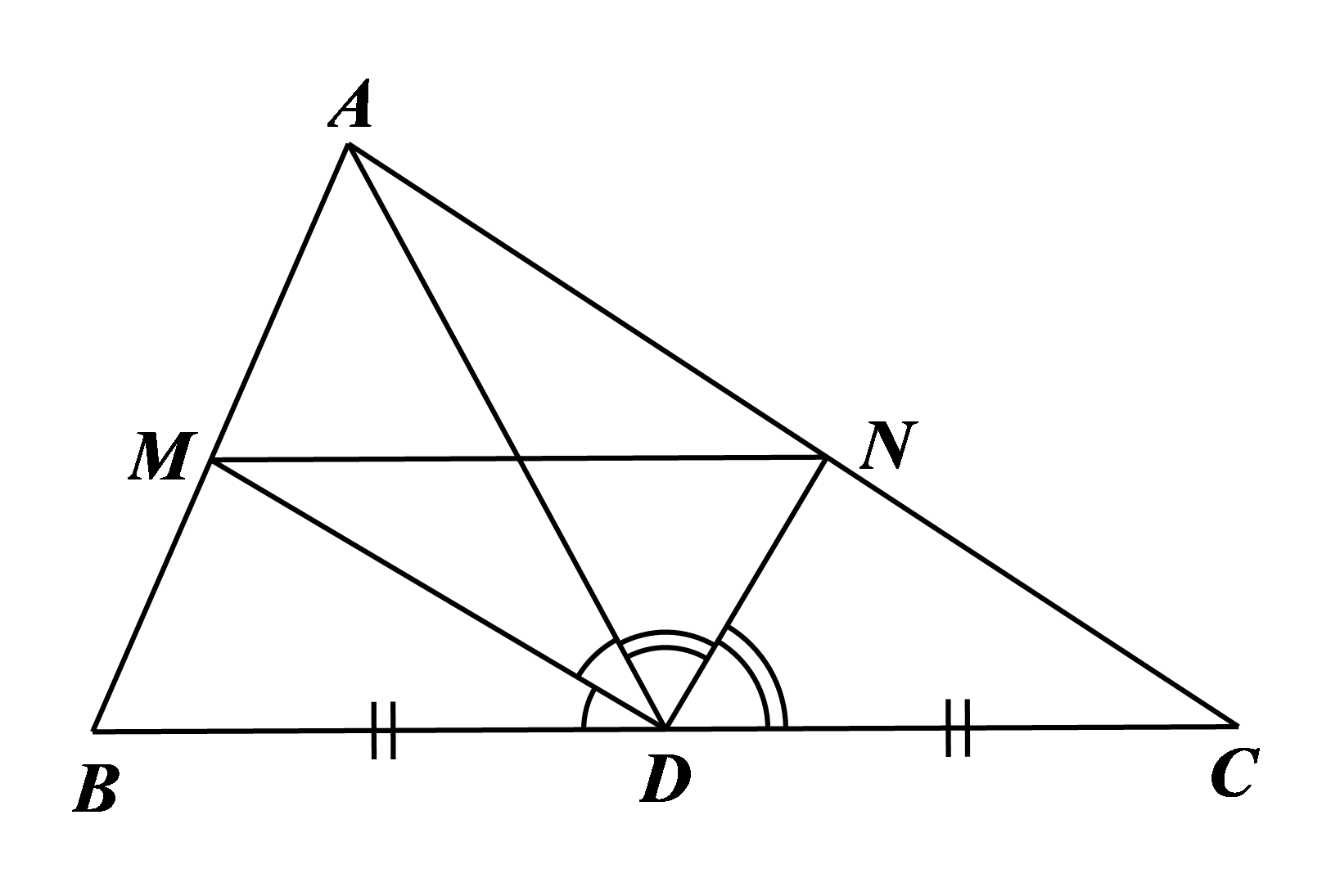
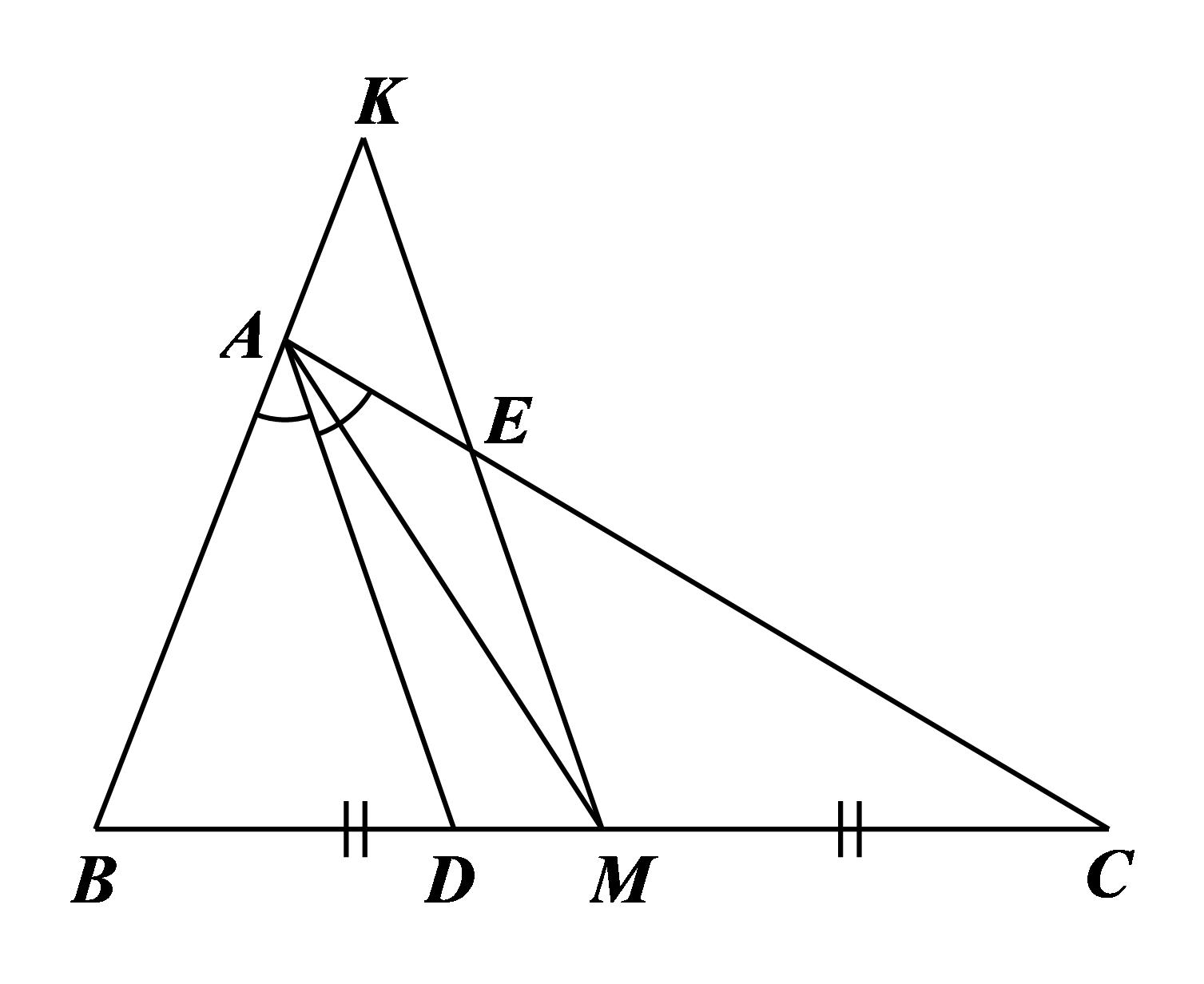
![Cho tứ giác \[ABCD.\] Gọi \[E,{\rm{ }} (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/33-1764811231.png)