10 Bài tập Chứng minh các tính chất hình học (có lời giải)
53 người thi tuần này 4.6 373 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
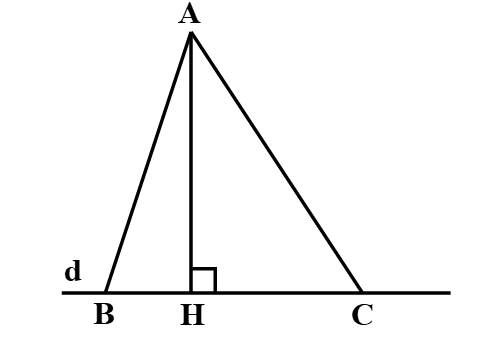
Câu 1
A. Trong tam giác vuông, cạnh huyền là cạnh lớn nhất;
B. Trong tam giác vuông, cạnh huyền là cạnh bé nhất;
C. Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
Vẽ tam giác ABC vuông tại A.
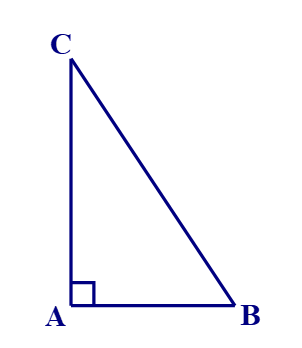
Áp dụng định lí Pythagore vào tam giác vuông ABC ta được:
BC2 = AC2 + AB2
Þ AC < BC, AB < BC
Mà BC là cạnh huyền và AB, AC là các cạnh góc vuông.
Vậy trong giác vuông cạnh huyền là cạnh lớn nhất.
Câu 2
A. HB > HC thì AB > AC;
B. HB > HC thì AB = AC;
C. HB < HC thì AB > AC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
Áp dụng định lí Pythagore trong tam giác vuông AHB và AHC ta có:
AB2 = AH2 + BH2
AC2 = AH2 + CH2
+) Nếu BH < CH thì AB < AC.
+) Nếu BH > CH thì AB > AC.
Vậy khẳng định đúng là HB > HC thì AB > AC.
Câu 3
A. AH < BH;
B. AH < AB;
C. AH > BH;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
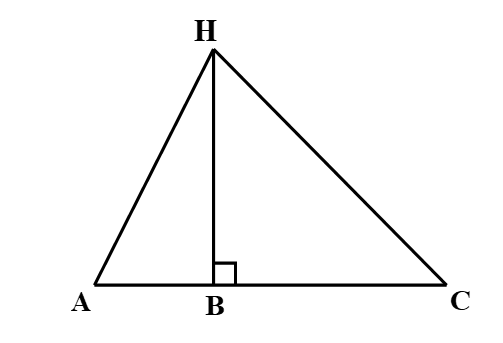
Áp dụng định lí Pythagore vào tam giác HBA vuông ở B ta có:
AH2 = BH2 + AB2
Þ AH > AB, AH > BH.
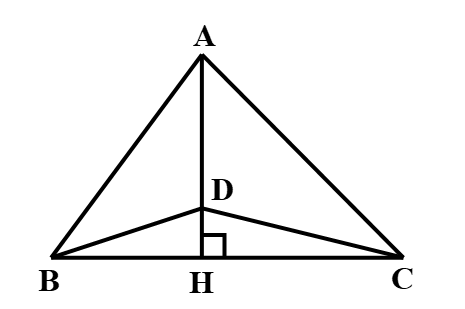
Câu 4
A. Nếu HB < HC thì BD > DC;
B. Nếu HB < HC thì BD < DC;
C. Nếu HB = HC thì BD < DC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
*) Áp dụng định lí Pythagore vào tam giác vuông AHB và AHC ta có:
AB2 = AH2 + BH2
AC2 = AH2 + CH2
Vì AB < AC nên BH < CH.
*) Áp dụng định lí Pythagore vào tam giác vuông BHD và BHC ta có:
BD2 = BH2 + DH2
CD2 = CH2 + DH2
Vì BH < CH nên BD < CD.
Câu 5
A. Chỉ có (I) đúng;
B. Chỉ có (II) đúng;
C. Cả (I) và (II) đều đúng;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
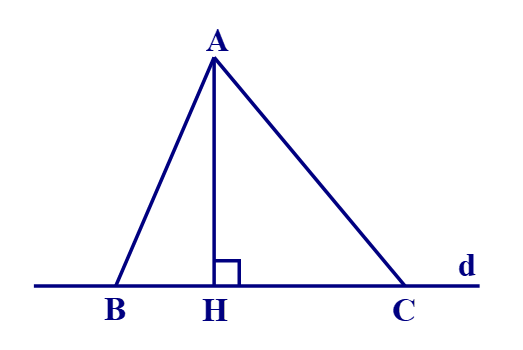
+) Vì tam giác AHB vuông nên AH < AB.
+) Vì tam giác ACH vuông nên AH < AC.
Þ Khẳng định (I) đúng.
+) Áp dụng định lí Pythagore vào tam giác vuông AHB và AHC ta được:
AB2 = AH2 + BH2
AC2 = AH2 + CH2
Nếu AB2 < AC2 thì AB < AC. Suy ra, BH < CH.
Nếu AB2 > AC2 thì AB > AC. Suy ra, BH > CH.
Do đó, BH < CH hoặc BH > CH.
Þ Khẳng định (II) sai.
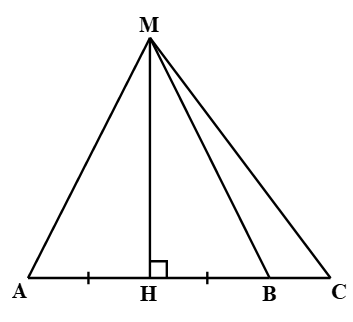
Câu 6
A. BC vuông góc MH;
B. BC trùng với MH;
C. BC song song với MH;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
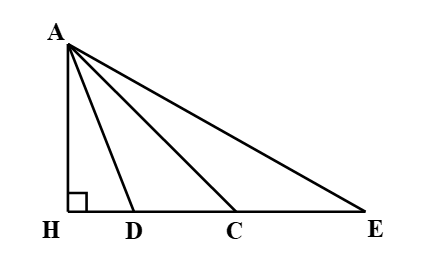
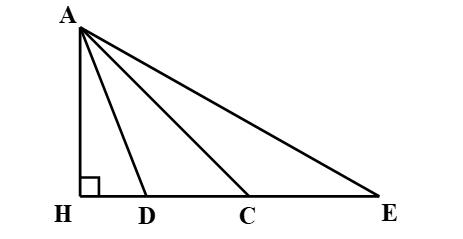
Câu 9
A. Vì HD < HC < HE nên AD > AC > AE;
B. Vì HD > HC > HE nên AD > AC > AE;
C. Vì HD < HC < HE nên AD < AC < AE;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. MA > MH;
B. HB < HC;
C. MA = MB;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.