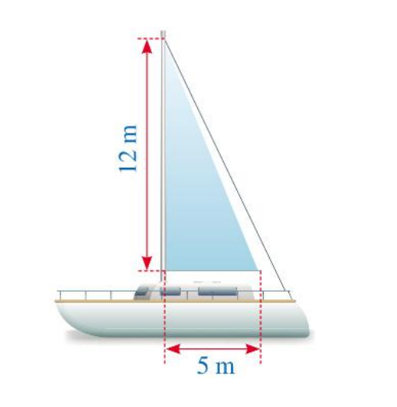
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
225 người thi tuần này 4.6 10 K lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 02
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 01
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
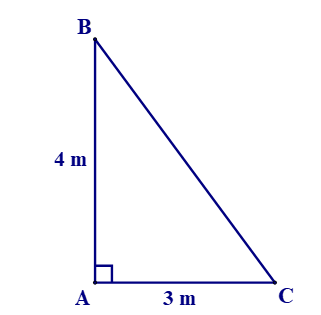
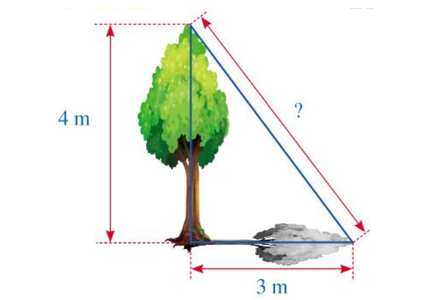
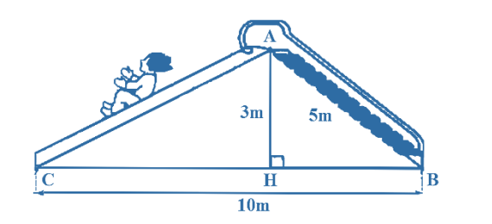
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AB2 + AC2 = 42 + 32 = 25
BC = 5 m
Vậy khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây là 5 m.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
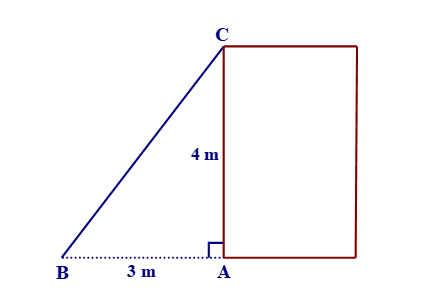
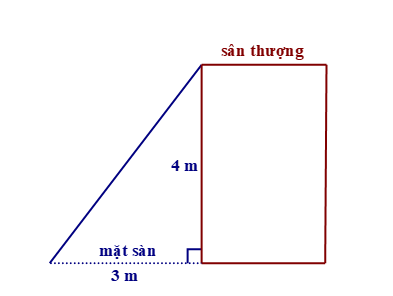
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AC2 + AB2 = 42 + 32 = 25
BC = 5 m.
Câu 3
A. AB 43,2 dm;
B. AB 43,3 dm;
C. AB 44,2 dm;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
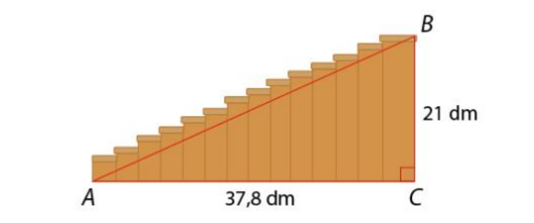
Xét tam giác ABC vuông tại C, áp dụng định lý Pythagore ta có:
AB2 = BC2 + AC2 = 212 + 37,82 = 1 869,84
AB 43,2 dm
Vậy độ dài AB là 43,2 dm.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
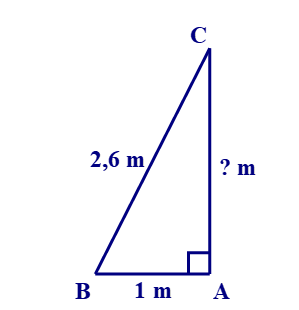
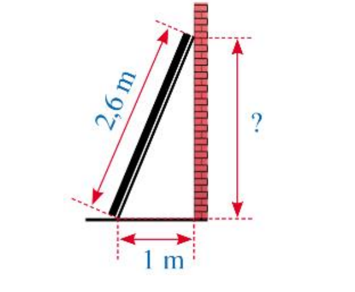
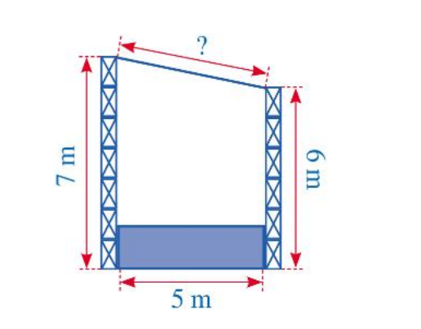
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:
BC2 = AC2 + AB2
AC2 = BC2 – AB2 = 2,62 – 12 = 5,76
AC = 2,4 m.
Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là 2,4 m.
Lời giải

Câu 6
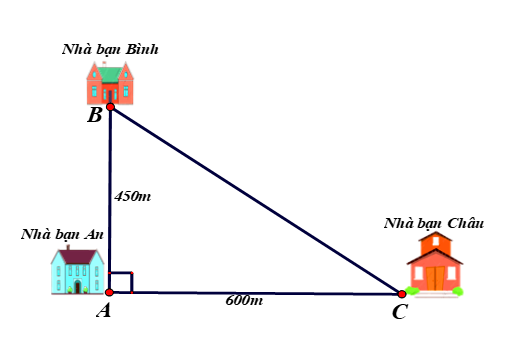
A. 300 m;
B. 450 m;
C. 600 m;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
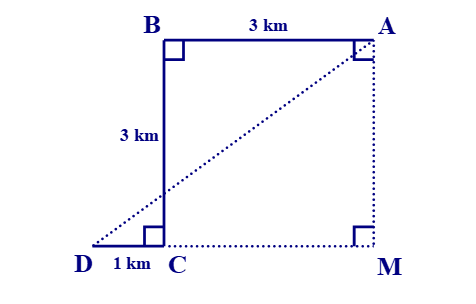
A. 5 km;
B. 5 m;
C. 3 km;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 5,0;
B. 5,1;
C. 5,2;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 13 m;
B. 15 m;
C. 40 m;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 101,4 m;
B. 102,4 m;
C. 102,3 m;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.