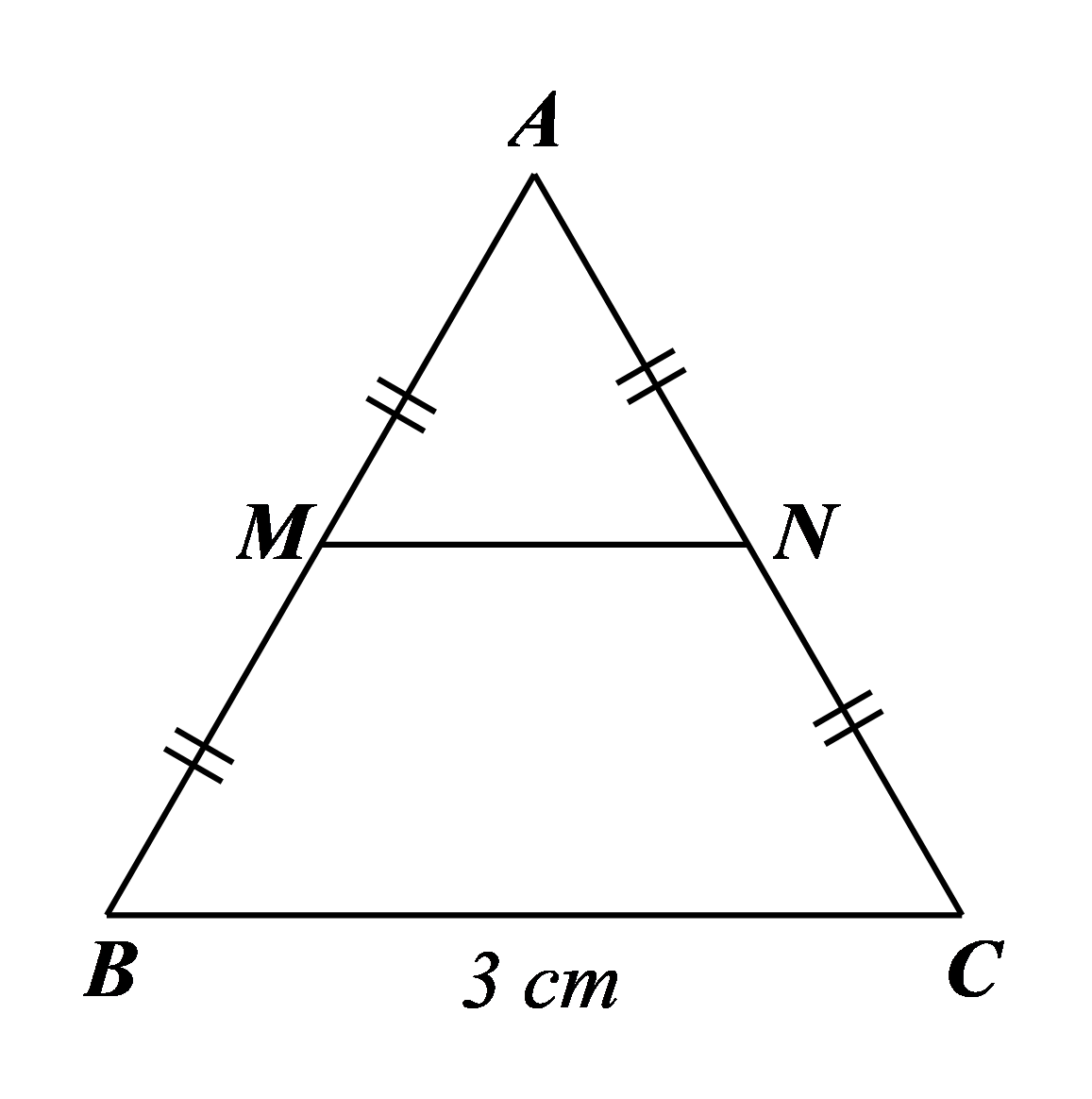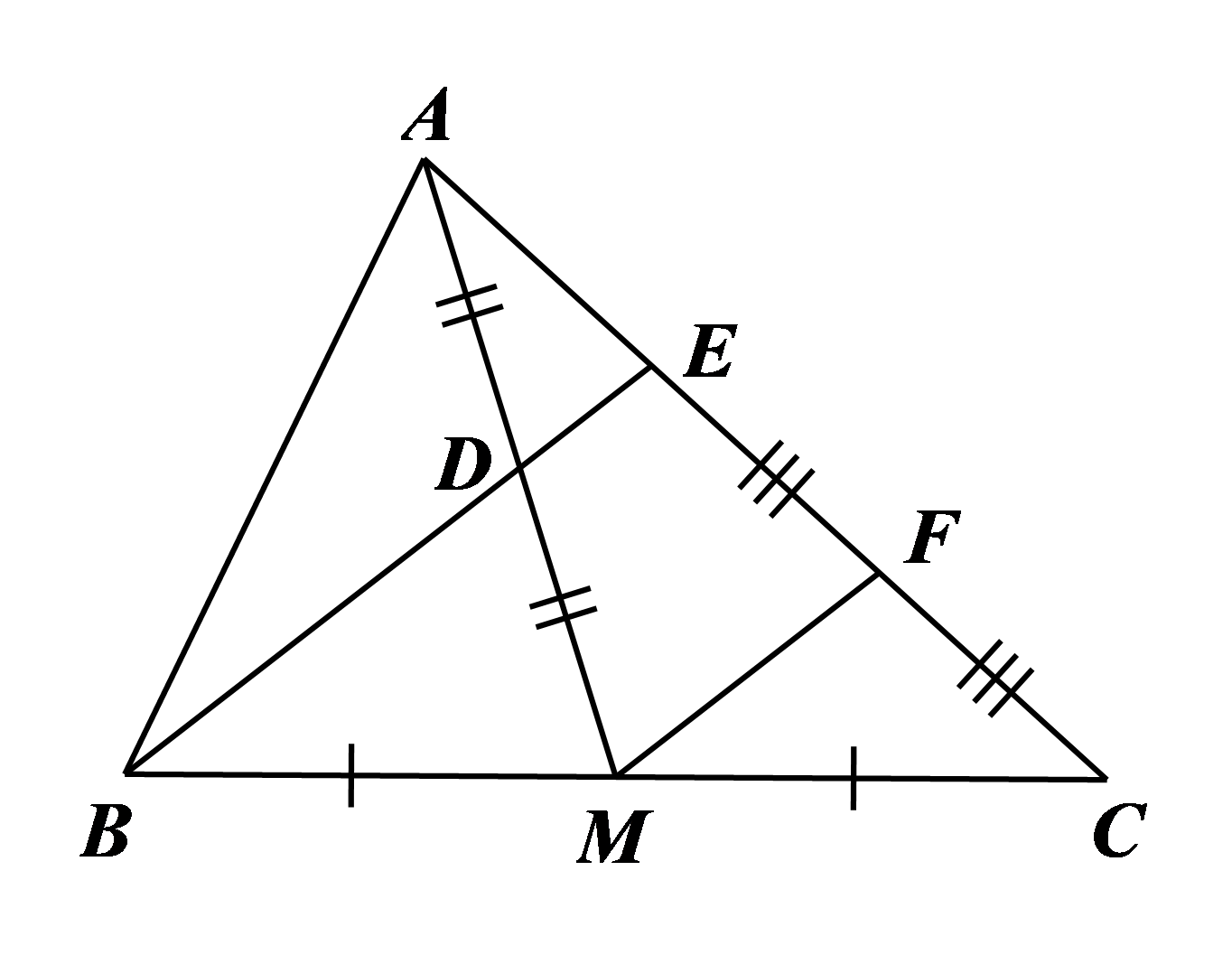Cho \(\Delta ABC\) đều cạnh \(3{\rm{\;cm}}.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB\) và \(AC.\) Chu vi của tứ giác \(MNCB\) là
A. \(8{\rm{\;cm}}.\)
B. \(7,5{\rm{\;cm}}.\)
C. \(6{\rm{\;cm}}.\)
D. \(7{\rm{\;cm}}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Hướng dẫn giải Đáp án đúng là: B Vì \(\Delta ABC\) đều cạnh \(3{\rm{\;cm}}\) nên \(AC = BC = CA = 3{\rm{\;cm}}{\rm{.}}\) Xét \(\Delta ABC\) có \(M,\,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\) nên \(MN\) là đường trung bình của tam giác, do đó \(\frac{{MN}}{{BC}} = \frac{1}{2},\) suy ra \(MN = \frac{{BC}}{2} = \frac{3}{2} = 1,5{\rm{\;cm}}.\) |
|
Vì \(M,\,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\) nên ta có \(BM = \frac{1}{2}AB = \frac{1}{2}AC = NC,\) do đó \(BM = NC = 1,5{\rm{\;cm}}.\)
Vậy chu vi của tứ giác \(MNCD\) là:
\(MN + NC + BC + BM = 1,5 + 1,5 + 3 + 1,5 = 7,5{\rm{\;(cm)}}{\rm{.}}\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(4,5{\rm{\;cm}}.\)
B. \(3{\rm{\;cm}}.\)
C. \(2{\rm{\;cm}}.\)
D. \(6{\rm{\;cm}}.\)
Lời giải
|
Hướng dẫn giải Đáp án đúng là: B Xét \[\Delta BCE\] có \(M,\,\,F\) lần lượt là trung điểm của \(BC,\,\,EC\) nên \(MF\) là đường trung bình của tam giác, do đó \(MF\,{\rm{//}}\,BE,\) hay \(MF\,{\rm{//}}\,DE.\) |
|
Xét \(\Delta AMF\) có \(D\) là trung điểm của \(AM\) và \(DE\,{\rm{//}}\,MF\) nên \(DE\) là đường trung bình của tam giác, do đó \(E\) là trung điểm của \(AF.\) Suy ra \(AE = EF.\)
Mà \(F\) là trung điểm của \(EC\) nên \(EF = FC,\) do đó \(AE = EF = FC\) hay \(AE = \frac{1}{3}AC = \frac{1}{3} \cdot 9 = 3{\rm{\;cm}}.\)
Câu 2
A. \(4{\rm{\;cm}}.\)
B. \(4,5{\rm{\;cm}}.\)
C. \(3,5{\rm{\;cm}}.\)
D. \(14{\rm{\;cm}}.\)
Lời giải
Đáp án đúng là: A
Xét \(\Delta ABC\) có \(I,\,\,K\) lần lượt là trung điểm của \(AB\) và \(AC\) nên \(IK\) là đường trung bình của tam giác, do đó \(\frac{{IK}}{{BC}} = \frac{1}{2},\) suy ra \(IK = \frac{{BC}}{2} = \frac{8}{2} = 4{\rm{\;cm}}.\)
Câu 3
A. \(m \ne \frac{3}{4}.\)
B. \(m \ne - \frac{3}{4}.\)
C. \(m \ne \frac{4}{3}.\)
D. \(m \ne - \frac{4}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{5}{8}.\)
B. \(\frac{5}{{11}}.\)
C. \(\frac{3}{{11}}.\)
D. \(\frac{8}{{11}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\[4x + 6 = 0.\]
B.
C.
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(20{\rm{\;cm}}.\)
B. \(\frac{{18}}{{25}}{\rm{\;cm}}.\)
C. \(50{\rm{\;cm}}.\)
D. \(45{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập