Một chất điểm đang dao động điều hòa dọc theo trục Ox, mốc tính thế năng tại vị trí cân bằng O. Từ thời điểm t1=0 đến thời điểm t2, quả cầu của con lắc đi được quãng đường S và chưa đổi chiều chuyển động, đồng thời động năng của con lắc giảm từ giá trị cực đại về 0,6J. Từ thời điểm t2 đến thời điểm t3, chất điểm đi thêm một đoạn đường 2S nữa mà chưa đổi chiều chuyển động và động năng của con lắc vào thời điểm t3 là 0,28J. Từ thời điểm t3 đến t4 chất điểm đi thêm đoạn đường bằng 3S nữa thì động năng của chất điểm vào thời điểm t4 bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Phương pháp giải
Sử dụng vòng tròn lượng giác biểu diễn các thời điểm.
Động năng của chất điểm: \({W_d} = \frac{1}{2}k\left( {{A^2} - {x^2}} \right)\)
Lời giải
Ở thời điểm t1, động năng của chất điểm có giá trị cực đại, khi đó vật ở vị trí cân bằng.
Ta có vòng tròn lượng giác:
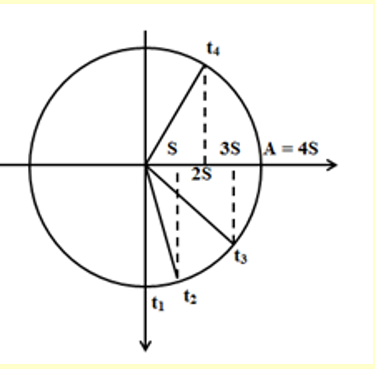
\[\left\{ {\begin{array}{*{20}{l}}{{x_2} = S}\\{{x_3} = S + 2S = 3S}\end{array}} \right.\]
Động năng của chất điểm ở thời điểm t2 và t3 là:
\(\left\{ {\begin{array}{*{20}{l}}{{W_{{d_2}}} = \frac{1}{2}k\left( {{A^2} - x_2^2} \right)\,\,\left( 1 \right)}\\{{W_{{d_3}}} = \frac{1}{2}k\left( {{A^2} - x_3^2} \right)\,\,\,\left( 2 \right)}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{2}k\left( {{A^2} - {S^2}} \right) = 0,6}\\{\frac{1}{2}k\left( {{A^2} - 9{S^2}} \right) = 0,28}\end{array}} \right.\)
\( \Rightarrow \frac{{{A^2} - {S^2}}}{{{A^2} - 9{S^2}}} = \frac{{0,6}}{{0,28}} \Rightarrow S = \frac{A}{4}\)
Thay \(S = \frac{A}{4}\) vào phương trình (1), ta có:
\(\frac{1}{2}k\left[ {{A^2} - {{\left( {\frac{A}{4}} \right)}^2}} \right] = 0,6 \Rightarrow \frac{{15}}{{32}}k{A^2} = 0,6 \Rightarrow k{A^2} = 1,28\)
Từ thời điểm t1 đến thời điểm t4, quãng đường chất điểm chuyển động là:
\({S^\prime } = S + 2S + 3S = 6S = 6.\frac{A}{4} = \frac{{3A}}{2}\)
Li độ của chất điểm ở thời điểm t4 là: \({x_4} = {S^\prime } - A = \frac{{3A}}{2} - A = \frac{A}{2}\)
Động năng của chất điểm lúc này là:
\({W_{{d_4}}} = \frac{1}{2}k\left( {{A^2} - {x_4}^2} \right) = \frac{1}{2}k\left[ {{A^2} - {{\left( {\frac{A}{2}} \right)}^2}} \right] = \frac{3}{8}k{A^2} = \frac{3}{8}.1,28 = 0,48(J)\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là A
Phương pháp giải
Vận dụng lý thuyết về mô hình động học phân tử chất khí
Lời giải
Bình xịt khử trùng: Khí bên trong bình được nén dưới áp suất cao. Khi ta ấn nút, van mở, khí
thoát ra ngoài, thể tích khí tăng. Áp suất khí giảm, tạo ra lực đẩy giúp phun dung dịch khử trùng.
Lời giải
Đáp án đúng là C
Phương pháp giải
Tính khối lượng chloramine cần để khử khuẩn cho bể nước có dung tích 2,5m3 rồi tình số viên chloamine B cần dùng.
Lời giải
Để khử khuẩn bể nước có dung tích là 2,5m3 cần khối lượng chloramine là: \(\frac{{2,{{5.10}^3}}}{{1000}}.10 = 25{\rm{gam}}\)
Môi viên nén có chứa 250mg chloramine B nên số viên chloramine B cần là: \(\frac{{{{25.10}^3}}}{{250}} = 100\) viên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập