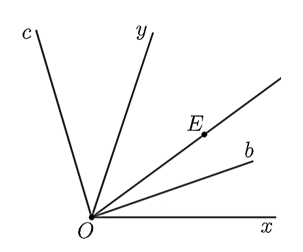
Cho \(\widehat {aOb}\) là góc vuông. Gọi \(Oc,\;\,Od\) lần lượt là tia đối của các tia \(Oa,\;\,Ob.\) Khi đó:
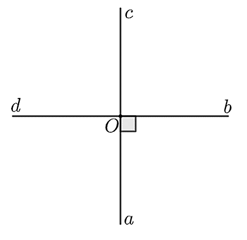
Cho \(\widehat {aOb}\) là góc vuông. Gọi \(Oc,\;\,Od\) lần lượt là tia đối của các tia \(Oa,\;\,Ob.\) Khi đó:
a) \(\widehat {aOb} = \widehat {cOd} = 90^\circ .\)
Đúng
Sai
b) \(\widehat {aOc}\) là góc bẹt.
Đúng
Sai
c) Có tất cả 4 góc vuông.
Đúng
Sai
d) Số góc bẹt bằng số góc vuông.
Đúng
Sai
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng.
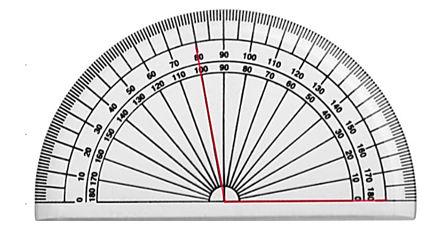
Vì \(\widehat {aOb}\) là góc vuông nên \(\widehat {aOb} = 90^\circ .\) Dùng thước đo góc ta đo được \(\widehat {cOd} = 90^\circ .\)
Vậy \(\widehat {aOb} = \widehat {cOd} = 90^\circ .\)
b) Đúng.
Vì \(Oa\) và \(Oc\) là hai tia đối nhau nên \(\widehat {aOc}\) là góc bẹt. Vậy \(\widehat {aOc}\) là góc bẹt.
c) Đúng.
Có tất cả 4 góc vuông là: \(\widehat {aOb};\;\,\widehat {cOd};\;\,\widehat {cOb};\;\,\widehat {aOd}.\) Vậy có tất cả 4 góc vuông.
d) Sai.
Có tất cả 2 góc bẹt là \(\widehat {aOc}\) và \(\widehat {bOd}.\) Vậy số góc bẹt ít hơn số góc vuông.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 6 giờ 30 phút.
B. 6 giờ.
C. 12 giờ 30 phút.
D. 9 giờ.
Lời giải
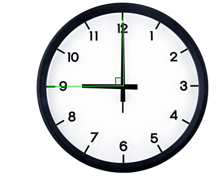
Đáp án đúng là: D
Vào lúc 9 giờ, kim giờ và kim phút tạo thành một góc vuông.
Câu 3
a) \(\widehat B\) là góc nhọn.
Đúng
Sai
b) \(\widehat C = 140^\circ .\)
Đúng
Sai
c) \(\widehat D\) có số đo lớn hơn \(90^\circ .\)
Đúng
Sai
d) Tổng 4 góc trong tứ giác \(ABCD\) bằng \(350^\circ .\)
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(80^\circ .\)
B. \(90^\circ .\)
C. \(100^\circ .\)
D. \(110^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\widehat A.\)
B. \(\widehat B.\)
C. \(\widehat C.\)
D. \(\widehat D.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập