a) Giải phương trình: \(x = \frac{5}{{x - 1}} + 2\sqrt {x - 2} \).

b) Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{\frac{{9y + 49}}{{x + y}} + x + y = 23\;\;\;\;\;\;\;\;\;\;\;\;}\\{x\sqrt x + y\sqrt y = 7(\sqrt x + \sqrt {y)} \;}\end{array}} \right.\)

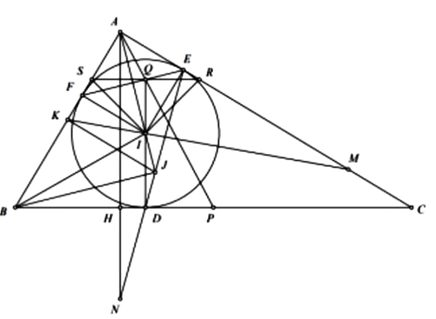
a) Ta có \(CD = CE\) nên tam giác \(CDE\) cân tại C. Suy ra \(\widehat {CDE} = \widehat {CED} = \) \(\frac{{{{180}^0} - \widehat {ACB}}}{2}\).

Áp dụng tính chất góc ngoài trong tam giác AJE, ta thấy

 \(\widehat {AJE} = \widehat {CEJ} = \widehat {EAJ} = \) \(\frac{{{{180}^0} - \widehat {ACB}}}{2} - \frac{{\widehat {BAC}}}{2} = \frac{{\widehat {ABC}}}{2}\) = \(\widehat {IBD}\). Suy ra tứ giác BIJD nội tiếp.

b) Do tứ giác BIJD nội tiếp nên \(\widehat {BJI} = \widehat {BDI} = {90^0}.\)

Vì \(\widehat {AJB} = {90^0}\) và \(\widehat {JAB} = \frac{{\widehat {BAC}}}{2} = {45^0}\) nên tam giác JAB vuông cân tại J. Theo giả thiết K là trung điểm của AB, ta có \(JK \bot AB\)

Chú ý rằng \(IF\parallel AM\parallel JK\) (cùng vuông góc với AB) và \(ID\parallel AH\) (cùng vuông góc với BC), ta có

\(\frac{{IF}}{{AM}} = \frac{{KI}}{{KM}} = \frac{{JI}}{{JA}} = \frac{{ID}}{{AN}}.\;\)Vì \(IF = ID\) nên \(AM = AN.\)

c) Đường thẳng qua Q vuông góc với ID cắt AC, AB lần lượt lại R, S.

Vì \(\widehat {IQR} = \widehat {IQS} = \widehat {IER} = \widehat {IFS} = {90^0}\) nên các tứ giác IQER, IQSR nội tiếp. Chú ý rằng tam giác IEF cân tại I, ta có \(\widehat {IRQ} = \widehat {IEQ} = \widehat {IFQ} = \widehat {ISQ}.\) Suy ra, tam giác IRS cân tại I. Do \(IQ \bot RS\) nên Q là trung điểm của RS.

Ta có \(RS\parallel BC\) (cùng vuông góc với ID) và P, Q lần lượt là trung điểm của BC, RS nên A, P, Q thẳng hàng (theo bồ đề hình thang).

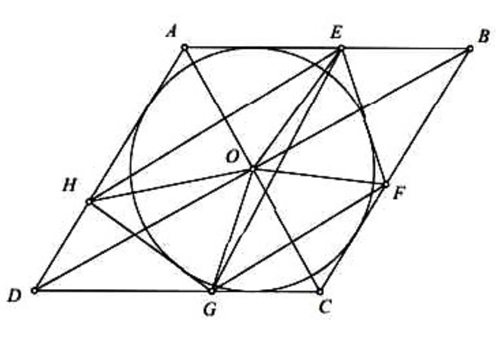
a) Đường tròn (O) tiếp xúc với các cạnh của hình thoi ABCD nên O là trung điểm của hai đường chéo AC và BD.

Ta thấy O là tâm đường tròn bàng tiếp góc D của tam giác DGH. Suy ra \(\widehat {GOH} = {180^0} - \widehat {OGH} - \widehat {OHG}\) = \({180^0} - \) \(\frac{{{{180}^0} - \widehat {DGH}}}{2} - \frac{{{{180}^0} - \widehat {DHG}}}{2}\) = \(\frac{{\widehat {DHG} + \widehat {DGH}}}{2} = \frac{{{{180}^0} - \widehat {GDH}}}{2}\).

Do tam giác \(DAC\) cân tại D nên \(\widehat {DAC} = \widehat {DCA}\) = \(\frac{{{{180}^0} - \widehat {ADC}}}{2}\). Kết hợp hai điều trên, ta thấy

                                      \(\widehat {GOH} = \widehat {DAC} = \widehat {DCA}.\)

Từ đó \(\widehat {COG} = {180^0} - \widehat {GOH} - \widehat {AOH} = {180^0} - \widehat {OAH} - \widehat {AOH} = \widehat {AHO}.\)

Suy ra hai tam giác OAH và GCO đồng dạng góc-góc. Vì thế, \(\frac{{OA}}{{GC}} = \frac{{AH}}{{CO}}.\)

Suy ra \(AH.CG = OA.OC = O{A^2}\).

b) Chứng minh tương tự ý trên, ta có \(AE.CF = O{A^2} = AH.CG\). Suy ra \(\frac{{AE}}{{CK}} = \frac{{AH}}{{CF}}\). Chú ý rằng \(\widehat {EAH} = \widehat {GCF}\), ta thu được hai tam giác AEH và CGF đồng dạng cạnh-góc-cạnh. Suy ra \(\widehat {AEH} = \widehat {CGF}.\) Lại có \(\widehat {AEG} = \widehat {CGE}\) (do \(AB\parallel CD\)). Suy ra \(\widehat {HEG} = \widehat {FGE}.\)

Vậy \(EH\parallel FG\) (đpcm).