1.Giải phương trình và hệ phương trình sau:
a) b)\(\left\{ \begin{array}{l}2x - y = 3\\3x + 2y = 1\end{array} \right.\)
2. Cho phương trình\[{x^2} - 2\left( {m--1} \right)x + {m^2}--4 = 0\], với \[m\]là tham số.
a) Tìm \[m\]để phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm \[{x_1},{x_2},\]tìm tất cả các giá trị của m để biểu thức \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\) đạt giá trị nhỏ nhất.
1.Giải phương trình và hệ phương trình sau:
a) b)\(\left\{ \begin{array}{l}2x - y = 3\\3x + 2y = 1\end{array} \right.\)
2. Cho phương trình\[{x^2} - 2\left( {m--1} \right)x + {m^2}--4 = 0\], với \[m\]là tham số.
a) Tìm \[m\]để phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm \[{x_1},{x_2},\]tìm tất cả các giá trị của m để biểu thức \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\) đạt giá trị nhỏ nhất.
Quảng cáo
Trả lời:
Cách giải:
1. Giải phương trình và hệ phương trình sau:
a) \[{x^4}--3{x^2}--4 = 0\left( 1 \right)\]
Đặt \[t = {x^2}(t \ge 0)\]
Khi đó \[\left( 1 \right) \Leftrightarrow {t^2}--3t--4 = 0\]
Do \[a--b + c = 1--\left( {--3} \right)--4 = 0\]nên phương trình có 2 nghiệm phân biệt\(\left[ \begin{array}{l}{t_1} = - 1(ktm)\\{t_2} = 4(tm)\end{array} \right.\)
Với \(t = 4 \Rightarrow {x^2} = 4 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\end{array} \right.\) (thỏa mãn)
Vậy tập nghiệm của phương trình là \[S = \left\{ {--2;2} \right\}.\]
b) \(\left\{ \begin{array}{l}2x - y = 3\\3x + 2y = 1\end{array} \right.\)
Ta có\(\left\{ \begin{array}{l}2x - y = 3\\3x + 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 2y = 6\\3x + 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 7\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2x - 3 = 2 - 3 = - 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm \[\left( {x;y} \right) = \left( {1; - 1} \right).\]
2. Cho phương trình\[{x^2} - 2\left( {m--1} \right)x + {m^2}--4 = 0\], với \[m\]là tham số.
a) Tìm \[m\]để phương trình có hai nghiệm phân biệt.
Xét \[\Delta ' = {\left( {m--1} \right)^2}--1\left( {{m^2}--4} \right) = {m^2}--2m + 1--{m^2} + 4 = 5--2m\]
Để phương trình có hai nghiệm phân biệt thì
Vậy \(m < \frac{5}{2}\) thì phương trình có hai nghiệm phân biệt.
b) Khi phương trình có hai nghiệm\[{x_1},{x_2}\], tìm tất cả các giá trị của m để biểu thức \(P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2}\)đạt giá trị nhỏ nhất.
Để phương trình có \[2\] nghiệm \[{x_1},{x_2},\]thì
Khi đó áp dụng hệ thức Vi-et ta có\(\left\{ \begin{array}{l}{x_1} + {x_2} = 2(m - 1)\\{x_1}.{x_2} = {m^2} - 4\end{array} \right.\)
Ta có
\(\begin{array}{l}P = x_1^2 + x_2^2 + {x_1}{x_2} + {m^2} = x_1^2 + 2{x_1}{x_2} + x_2^2 - {x_1}{x_2} + {m^2}\\ = {({x_1} + {x_2})^2} - {x_1}{x_2} + {m^2}\\ = \left[ {2{{\left( {m - 1} \right)}^2}} \right] - ({m^2} - 4) + {m^2}\\ = 4{(m - 1)^2} - {m^2} + 4 + {m^2}\\ = 4{(m - 1)^2} + 4\end{array}\)
Do \({(m - 1)^2} \ge 0\,\forall m \Rightarrow 4{(m - 1)^2} + 4 \ge 4 \Rightarrow P \ge 4\)
Dấu bằng xảy ra khi \(m = 1\) (thỏa mãn \(m \le \frac{5}{2}\))
Vậy \({P_{\min }} = 4\) khi \(m = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hai đội công nhân cùng thi công một đoạn đường nông thôn và dự định hoàn thành công việc đó trong \[16\]ngày. Khi làm được \[12\] ngày thì đội I được điều động đi làm việc ở nơi khác. Những ngày sau đó, đội II làm việc với năng suất gấp \[1,5\]lần năng suất ban đầu nên đã hoàn thành công việc đúng thời gian dự định. Hỏi theo năng suất ban đầu, nếu mỗi đội làm một mình thì phải bao nhiêu ngày mới hoàn thành công việc trên?
Cách giải:
Gọi thời gian đội I hoàn thành công việc một mình là \[x\left( {x > 16,ng\`a y} \right)\]
Gọi thời gian đội II hoàn + công việc một mình là \[y\left( {y > 16,ng\`a y} \right)\]
Một ngày đội I làm một mình được \[\frac{1}{x}\] (công việc)
Một ngày đội II làm một mình được \[\frac{1}{y}\] (công việc)
Suy ra \(1\) ngày \[2\] đội làm được \(\frac{1}{x} + \frac{1}{y}\) (công việc)
Do \[2\] đội cùng thi công đoạn đường thì hoàn thành công việc trong \[16\] ngày nên ta có phương trình
\(\frac{1}{x} + \frac{1}{y} = \frac{1}{{16}}\,(1)\)
Ta có \[2\] đội làm cùng nhau trong \[13\] ngày được \(12\left( {\frac{1}{x} + \frac{1}{y}} \right) = \frac{{12}}{{16}} = \frac{3}{4}\) (công việc)
Đội II tăng lên \[1,5\]lần nên mỗi ngày đội \[2\] làm được\[\frac{{1,5}}{y} = \frac{3}{{2y}}\] (công việc)
Đề hoàn thành công việc trong \[16\] ngày như dự định thì đội II phải hoàn thành nốt công việc trong \[4\] ngày
Khi đó ta có phương trình \(\frac{3}{4} + \frac{3}{{2y}}.4 = 1 \Leftrightarrow y = 24\)
Thay \(y = 24\) vào \[\left( 1 \right)\]ta được\(\frac{1}{x} + \frac{1}{{24}} = \frac{1}{{16}} \Rightarrow x = 48\)(ngày)
Vậy đội I hoàn thành công việc một mình trong \[48\] ngày, đội II hoàn thành công việc trong \[24\] ngày.
Lời giải
Cách giải:
1) Thực hiện phép tính \(3\sqrt {49} - \sqrt {121} \)
Ta có: 3\(\sqrt {49} \) – \(\sqrt {121} \) = 3.\(\sqrt {{7^2}} \) – \(\sqrt {{{11}^2}} \) = 3.7 – 11 = 21 – 11 = 10
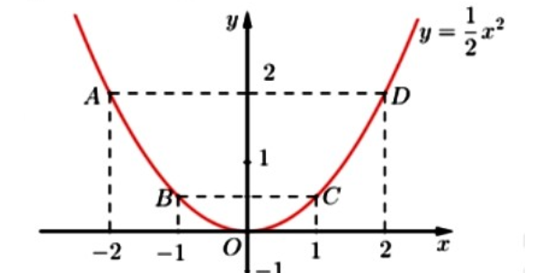
2) Vẽ đồ thị \[\left( P \right)\]của hàm số \[y = \frac{1}{2}{x^2}.\]
Ta có bảng giá trị sau:
|
\[x\] |
\[--2\] |
\[--1\] |
\[0\] |
\[1\] |
\[2\] |
|
\[y = \frac{1}{2}{x^2}\] |
\[2\] |
\(\frac{1}{2}\) |
\[0\] |
\(\frac{1}{2}\) |
\[2\] |
Þ Đồ thị hàm số là đường cong parabol đi qua các điểm \(O(0;0);A( - 2;2);B( - 1;\frac{1}{2});C(1;\frac{1}{2});D(2;2)\)
Hệ số \[a = \frac{1}{2} > 0\]nên parabol có bề cong hướng lên. Đồ thị hàm số nhận \[Oy\]làm trục đối xứng.
Ta vẽ được đồ thị hàm số \[y = \frac{1}{2}{x^2}\] như sau:
3. Cho hai đường thẳng \[\left( d \right):y = 2x + 1\]và \[\left( {d'} \right):y = ax + b\left( {a \ne 0} \right).\]Tìm \[a,b\]biết \[\left( {d'} \right)\]song song với \[\left( d \right)\]và đi qua điểm \[A\left( {2;3} \right).\]
Vì song song với \[\left( d \right)\]nên\(\left\{ \begin{array}{l}a = 2\\b \ne 1\end{array} \right.\) hay phương trình \[\left( {d'} \right)\]có dạng: \(y = 2x + b\)y=2 với \(b \ne 1\)
Vì \[\left( d \right)\]đi qua điểm \[A\left( {2;3} \right)\]nên thay tọa độ điểm \[A\]vào phương trình đường thẳng ta được:
\(3 = 2.2 + b \Leftrightarrow 3 = 4 + b \Leftrightarrow b = - 1\) (thỏa mãn \(b \ne 1\))
Vậy a = 2 và b = –1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![1.Cho tam giác \[ABC\]vuông tại\[A\], đường cao \[AH.\]Biết \[BH = 4cm,HC = 5cm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid2-1766929813.png)