Một doanh nghiệp kinh doanh một loại sản phẩm \[T\] được sản xuất trong nước. Qua nghiên cứu thấy rằng nếu chi phí sản xuất mỗi sản phẩm \[T\] là \[x\](\[\$ \]) thì số sản phẩm \[T\] các nhà máy sản xuất sẽ là \[R(x) = x - 200\] và số sản phẩm \[T\]mà doanh nghiệp bán được trên thị trường trong nước sẽ là \[Q(x) = 4200 - x\]. Số sản phẩm còn dư doanh nghiệp xuất khẩu ra thị trường quốc tế với giá bán mỗi sản phẩm ổn định trên thị trường quốc tế là \[{x_0} = 3200\]\[\$ \]. Nhà nước đánh thuế trên mỗi sản phẩm xuất khẩu là \[a\](\[\$ \]) và luôn đảm bảo tỉ lệ giữa lãi xuất khẩu của doanh nghiệp và thuế thu được của nhà nước tương ứng là \[4:1\]. Hãy xác định giá trị của \[a\] biết lãi mà doanh nghiệp thu được do xuất khẩu là nhiều nhất.
Một doanh nghiệp kinh doanh một loại sản phẩm \[T\] được sản xuất trong nước. Qua nghiên cứu thấy rằng nếu chi phí sản xuất mỗi sản phẩm \[T\] là \[x\](\[\$ \]) thì số sản phẩm \[T\] các nhà máy sản xuất sẽ là \[R(x) = x - 200\] và số sản phẩm \[T\]mà doanh nghiệp bán được trên thị trường trong nước sẽ là \[Q(x) = 4200 - x\]. Số sản phẩm còn dư doanh nghiệp xuất khẩu ra thị trường quốc tế với giá bán mỗi sản phẩm ổn định trên thị trường quốc tế là \[{x_0} = 3200\]\[\$ \]. Nhà nước đánh thuế trên mỗi sản phẩm xuất khẩu là \[a\](\[\$ \]) và luôn đảm bảo tỉ lệ giữa lãi xuất khẩu của doanh nghiệp và thuế thu được của nhà nước tương ứng là \[4:1\]. Hãy xác định giá trị của \[a\] biết lãi mà doanh nghiệp thu được do xuất khẩu là nhiều nhất.
Quảng cáo
Trả lời:
Đáp án:
Theo bài ta tính được số sản phẩm xuất khẩu là:
\[E(x) = R(x) - Q(x) = (x - 200) - (4200 - x) = 2x - 4400\] (sản phẩm)
Với điều kiện để có xuất khẩu: \[2x - 4400 > 0 \Rightarrow x > 2200\]
Lại có: Giá bán của mỗi sản phẩm xuất khẩu là \[{x_0} = 3200\]
Chi phí sản xuất mỗi sản phẩm là \[x\]
Thuế xuất khẩu mỗi sản phẩm là \[a\]
\[ \Rightarrow \]lãi trên mỗi sản phẩm xuất khẩu là \[3200 - x - a\](\[\$ \])
\[ \Rightarrow \]Tổng lãi xuất khẩu của doanh nghiệp là: \[L = (3200 - x - a)(2x - 4400)\]
Và tổng thuế nhà nước thu được là: \[T = a(2x - 4400)\]
Theo bài ta có tỉ lệ giữa lãi xuất khẩu của doanh nghiệp và thuế thu được của nhà nước tương ứng là \[4:1\] nên \[\frac{L}{T} = \frac{4}{1}\]\[ \Rightarrow \] \[\frac{{(3200 - x - a)(2x - 4400)}}{{a(2x - 4400)}} = \frac{4}{1}\]
Vì \[2x - 4400 > 0\] nên ta thu được \[\frac{{3200 - x - a}}{a} = \frac{4}{1}\]\[ \Rightarrow \]\[3200 - x - a = 4a\]\[ \Rightarrow \]\[a = \frac{{3200 - x}}{5}\]
Thay vào L ta thu được: \[L(x) = \left( {3200 - x - \frac{{3200 - x}}{5}} \right)\left( {2x - 4400} \right)\]
\[ \Rightarrow L(x) = \frac{4}{5}\left( {3200 - x} \right)\left( {2x - 4400} \right)\]\[ \Rightarrow L(x) = \frac{4}{5}\left( { - 2{x^2} + 10800x - 14080000} \right)\]
Hàm số \[L(x)\]là một tam thức bậc hai theo \[x\] với hệ số của \[{x^2}\] âm nên \[L(x)\]đạt giá trị lớn nhất tại đỉnh của Parabol
Hoành độ của tọa độ đỉnh là: \[x = \frac{{ - b}}{{2a}} = \frac{{10800}}{4} = 2700\](vì hệ số \[\frac{4}{5} > 0\] không làm thay đổi vị trí điểm cực đại)
Suy ra: Để lãi mà doanh nghiệp thu được do xuất khẩu là nhiều nhất thì giá trị của \[a\] là:
\[a = \frac{{3200 - 2700}}{5} = 100\](\[\$ \])
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
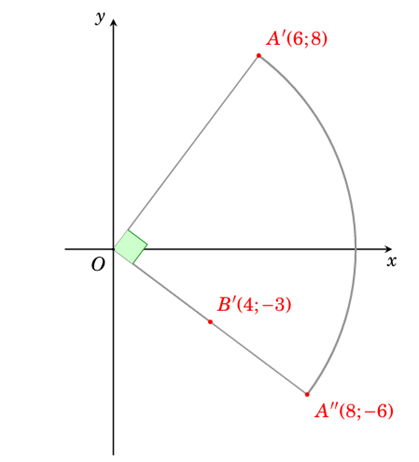
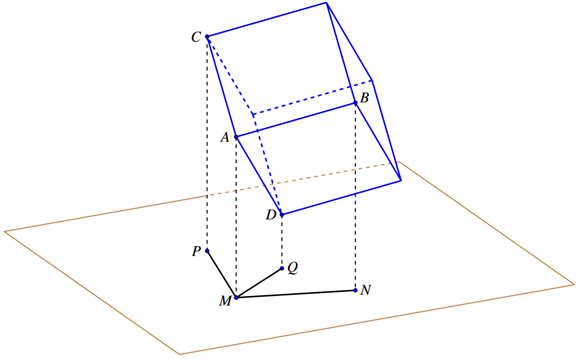
Gọi \(A'\), \(B'\) lần lượt là hình chiếu của điểm \(A\) và điểm \(B\) trên mặt phẳng \((Oxy)\).
Lúc đầu vật liệu ở vị trí \(A'(6;8)\) di chuyển thẳng đứng theo phương song song với phương của trục \(Oz\) một quãng đường \(16\,m\) (phải cao hơn độ cao \(15\,m\)của vị trí điểm đến \(1\,m\)).
Tiếp theo cẩu trục quay cần nâng di chuyển từ vị trí điểm \(A'\) đến vị trí điểm \(A''\) (di chuyển một góc có độ lớn \({90^^\circ }\)), khi đó vật liệu di chuyển một quãng đường:
\(l = R\alpha = OA' \cdot \frac{\pi }{2} = 10 \cdot \frac{\pi }{2} = 5\pi \) \(\left( m \right)\)
Tiếp đến điều chỉnh xe con nhằm di chuyển từ vị trí \(A''\) đến vị trí \(B'\) (với \(B'\) là trung điểm của \(OA''\)), tức là vật liệu di chuyển quãng đường \(A''B' = 5\,m\).
Cuối cùng móc cẩu hạ vật liệu xuống \(1\,m\) theo phương thẳng đứng đúng vị trí cần đặt là điểm \(B(4; - 3;15)\).
Vậy tổng quãng đường di chuyển của vật liệu là:
\(16 + 5\pi + 5 + 1 = 22 + 5\pi \approx 37,7\,m\).
Lời giải
![Nhà thầy Minh cách bờ biển Bãi Cháy \[1{\rm{km}}.\] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid10-1767804524.png)
Gọi nhà ở điểm \(A\), chợ ở điểm \(D\), đoạn trên bờ biển là \(BC = 500{\rm{m}}{\rm{.}}\)
Độ dài đoạn \(AH = 1000 - 400 = 600{\rm{m}}{\rm{, }}HD = \sqrt {D{A^2} - A{H^2}} = 800{\rm{m}}{\rm{.}}\)
Gọi \(M = {{\rm{T}}_{\overrightarrow {BC} }}(M),M'\) đối xứng với \(M\) qua bờ sông. Khi đó, \(MB = MC = M'C.\) Gọi \(C\) là giao điểm của \(M'D\) với bờ sông.
Ta được
\(\begin{array}{l}MB + BC + CD + DA = MC + 500 + CD + 1000 = 1500 + MC + CD\\ & = 1500 + M'C + CD \ge 1500 + M'D = 1500 + \sqrt {{{1400}^2} + {{200}^2}} \approx 2914{\rm{m}}{\rm{.}}\end{array}\)
Câu 3
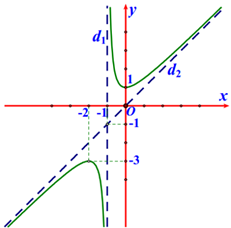
a) [NB] Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 1\).
b) [TH] Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
c) [TH] Đồ thị hàm số có 2 trục đối xứng, trong đó có một trục đối xứng là đường thẳng \(y = \left( {p + \sqrt q } \right)\left( {x + 1} \right) - r\) (\(p,q,r\)là các số nguyên). Khi đó \(p + q + r = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) [TH] Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( { - 2025;2026} \right)\).
b) [TH] Phương trình \(f\left( x \right) = 2013\) có nghiệm là \(x = e - 1\).
c) [NB] Tập xác định của hàm số \(y = f\left( x \right)\) là \(D = \left( { - 1; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Nhà thầy Minh cách bờ biển Bãi Cháy \[1{\rm{km}}.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid11-1767804532.png)