Nhà ông A cần làm một bể chứa nước có dạng khối hộp chữ nhật không nắp, có đáy là hình chữ nhật và chiều dài gấp ba lần chiều rộng, khối hộp tương ứng có thể tích bằng \(1152\,{\rm{d}}{{\rm{m}}^3}\). Giả sử bề dày của thành bể và đáy bể là không đáng kể. Giá thuê công nhân để làm bể là 400000 đồng/m2. Gọi \(x\) là chiều rộng của đáy bể (\(x\) là số dương và có đơn vị là dm). Các khẳng định sau đúng hay sai?
Nhà ông A cần làm một bể chứa nước có dạng khối hộp chữ nhật không nắp, có đáy là hình chữ nhật và chiều dài gấp ba lần chiều rộng, khối hộp tương ứng có thể tích bằng \(1152\,{\rm{d}}{{\rm{m}}^3}\). Giả sử bề dày của thành bể và đáy bể là không đáng kể. Giá thuê công nhân để làm bể là 400000 đồng/m2. Gọi \(x\) là chiều rộng của đáy bể (\(x\) là số dương và có đơn vị là dm). Các khẳng định sau đúng hay sai?
a) Chi phí thấp nhất mà ông A trả cho công nhân làm bể nước theo yêu cầu là 3072000 đồng.
b) Chiều cao của bể nước là \(\frac{{384}}{{{x^2}}}\) (dm).
c) Diện tích xung quanh của bể chứa nước là \(\frac{{3072}}{x}\,\left( {{\rm{d}}{{\rm{m}}^2}} \right)\).
Quảng cáo
Trả lời:
+ Theo bài ra ta có chiều dài của đáy bể nước là \(3x\).
Khi đó, chiều cao của bể là \(\frac{{384}}{{{x^2}}}\)
+ Diện tích xung quanh của bể chứa nước là
\(2\left( {x + 3x} \right).\frac{{384}}{{{x^2}}} = \frac{{3072}}{x}\).
Vậy, tổng diện tích cần làm của bể chứa nước là \(S\left( x \right) = \frac{{3072}}{x} + 3{x^2}\).
Ta có \(S'\left( x \right) = \frac{{3072}}{x} + 3{x^2} = \frac{{ - 3072 + 6{x^3}}}{{{x^2}}}\)
\(S'\left( x \right) = 0 \Rightarrow x = 8\)
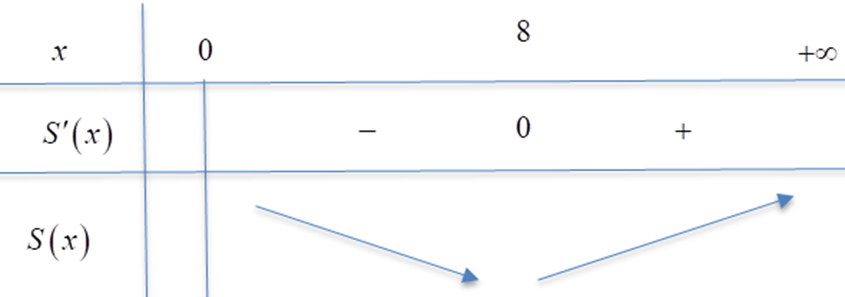
\(\mathop {\min }\limits_{0 \to + \infty } S\left( x \right) = S\left( 8 \right) = 576\,\left( {{\rm{d}}{{\rm{m}}^2}} \right) = 5,76\,\left( {{{\rm{m}}^2}} \right)\)
Chi phí thấp nhất là \(5,76\,.\,400000 = 2304000\) đồng.
Do đó a) sai, b) Đúng c) Đúng d) Sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
+) Khối lượng tôm giống vụ tôm vừa qua là 100kg
+) Gọi \[x\] là khối lượng tôm giống giảm đi.
+) Khối lượng tôm thu hoạch trong 1 kg/m2 tôm gống là \[2000:100 = 20{\rm{(kg)}}\].
+) Khi giảm đi 0,2kg/m2 tôm giống thì sản lượng thu hoạch tăng thêm trên \[1\,{{\rm{m}}^{\rm{2}}}\] là \[(2400 - 2000):100 = 4\,{\rm{kg/}}{{\rm{m}}^{\rm{2}}}\]
+) \[x\] là khối lượng tôm giống giảm đi suy ra số tôm giống cần thả là \[(100 - x)\,{\rm{kg}}\].
+) Sản lượng thu hoạch được trong 1kg tôm giống là \[(20 + ax){\rm{kg}}\]
Sản lượng thu hoạch được là \[f(x) = \left( {100 - x} \right)\left( {20 + ax} \right)\]
Ta biết cứ giảm đi 20 kg tôm giống thì thu hoạch được 2400 kg tôm suy ra \[f(20) = 2400\]
\[\left( {100 - 20} \right)(20 + a.20) = 2400 \Rightarrow a = 0,5 \Rightarrow f(x) = \left( {100 - x} \right)\left( {20 + 0,5{\rm{x}}} \right) = - 0,5{{\rm{x}}^2} + 30{\rm{x}} + 2000\]
Vậy \[f(x)\] đạt giá trị lớn nhất khi \[x = 30\].
Vậy cần phải thả là \[70\,{\rm{kg}}\] tôm giống.
Lời giải
Đáp án: 2,18.
Vì lúc 0 giờ sáng, số lượng vi khuẩn X là 150 con nên ta có: \[S\left( 0 \right) = 150 \Leftrightarrow A{e^{r.0}} = 150 \Leftrightarrow A = 150\] (con)
\[ \Rightarrow S\left( t \right) = 150{e^{rt}}\].
Sau 3 giờ, số lượng vi khuẩn X là 450 con nên \[S\left( 3 \right) = 450 \Leftrightarrow 150{e^{r.3}} = 450 \Leftrightarrow {e^{r.3}} = 3 \Leftrightarrow r = \frac{{\ln 3}}{3}\].
\[ \Rightarrow S\left( t \right) = 150{e^{\frac{{\ln 3}}{3}t}}\].
Vì số lượng vi khuẩn Y tăng 5% mỗi giờ nên số lượng vi khuẩn Y ở mỗi giờ theo thứ tự tạo thành một cấp số nhân có số hạng tổng quát là \[R\left( t \right) = 300{\left( {1 + 5\% } \right)^t}\].
Để số lượng vi khuẩn X bằng số lượng vi khuẩn Y thì \[S\left( t \right) = R\left( t \right)\].
\[ \Leftrightarrow 150{e^{\frac{{\ln 3}}{3}t}} = 300{\left( {1 + 5\% } \right)^t}\]
\[ \Leftrightarrow 150{e^{\frac{{\ln 3}}{3}t}} = 300{\left( {1,05} \right)^t}\].
\[ \Leftrightarrow \frac{{{e^{\frac{{\ln 3}}{3}t}}}}{{{{\left( {1,05} \right)}^t}}} = \frac{{300}}{{150}}\]\[ \Leftrightarrow \frac{{{e^{\frac{{\ln 3}}{3}t}}}}{{{{\left( {1,05} \right)}^t}}} = 2\].
\[ \Leftrightarrow {\left( {\frac{{{e^{\frac{{\ln 3}}{3}}}}}{{1,05}}} \right)^t} = 2\].
\[ \Leftrightarrow t = {\log _{\frac{{{e^{\frac{{\ln 3}}{3}}}}}{{1,05}}}}2 \approx 2,18\].
Vậy vào lúc 2,18 giờ thì số lượng vi khuẩn X bằng số lượng vi khuẩn Y.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
a) [VD,VDC] Xác suất chọn được 6 viên bi đủ ba màu, đồng thời ba số \(x - y,y - z,z - x\) theo thứ tự lập thành cấp số cộng là \(\frac{{40}}{{221}}\).
b) [TH] Xác suất chọn được ít nhất một viên bi màu xanh nhỏ hơn \(0,95\).
c) [TH] Xác suất chọn được 6 viên bi toàn màu xanh là \(\frac{1}{{2652}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Từ một tấm bìa mỏng hình lục giác đều cạnh \[4\sqrt 3 \;dm\], bạn An cắt bỏ sáu tam giác cân bằng nhau có cạnh đáy là cạnh của hình lục giác đều ban đầu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid9-1767809168.png)
![Một chiếc máy bay đang bay trong hệ trục toạ độ \[Oxyz\] với mặt phẳng \[(Oxy)\] là mặt đất như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid7-1767809067.png)