Một bệnh truyền nhiễm có xác suất lây bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Chị Hoa có tiếp xúc với người bệnh hai lần, một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất để chị Hoa bị lây bệnh từ người bệnh truyền nhiễm đó (nhập đáp án vào ô trống).

Đáp án  _____

Theo giả thiết, ta có: \(P\left( 0 \right) = - 25\).

\(P\left( {90} \right) = P\left( 0 \right) + \int\limits_0^{90} {P'\left( x \right)\,} {\rm{d}}x = - 25 + \int\limits_0^{90} {\left( {16 - 0,02x} \right)} \,{\rm{d}}x = - 25 + \left. {\left( {16x - 0,01{x^2}} \right)} \right|_0^{90} = 1\,334\).

Vậy nếu trong tuần nhà máy bán được 90 tấn sản phẩm thì thu được lợi nhuận là 1 334 triệu đồng.

Chọn hệ trục tọa độ như hình vẽ dưới.

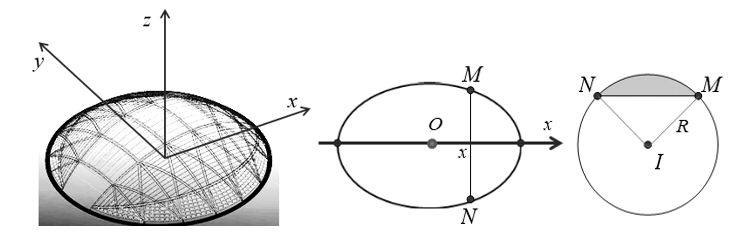
Ta cần tìm diện tích của \(S\left( x \right)\) thiết diện. Gọi \(d\left( {O,MN} \right) = x\).

Ta có \(\left( E \right):\frac{{{x^2}}}{{{{75}^2}}} + \frac{{{y^2}}}{{{{45}^2}}} = 1.\) Lúc đó \[MN = 2y = 2\sqrt {{{45}^2}\left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)} = 90\sqrt {1 - \frac{{{x^2}}}{{{{75}^2}}}} \]

\[ \Rightarrow R = \frac{{MN}}{{\sqrt 2 }} = \frac{{90}}{{\sqrt 2 }} \cdot \sqrt {1 - \frac{{{x^2}}}{{{{75}^2}}}} \Rightarrow {R^2} = \frac{{{{90}^2}}}{2} \cdot \left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)\].

Khi đó, \[S\left( x \right) = \frac{1}{4}\pi {R^2} - \frac{1}{2}{R^2} = \left( {\frac{1}{4}\pi - \frac{1}{2}} \right){R^2} = \left( {\pi - 2} \right)\frac{{2025}}{2} \cdot \left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right).\]

Thể tích khoảng không cần tìm là: \(V = \int\limits_{ - 75}^{75} {\left( {\pi - 2} \right)\frac{{2025}}{2} \cdot \left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)dx \approx 115\,\,586\,\,\left( {{m^3}} \right).} \) Chọn B.