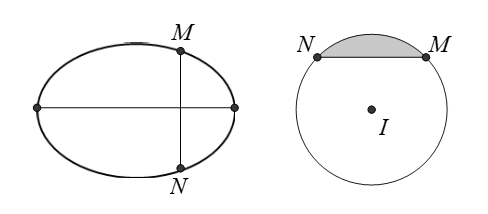
Một ca nô muốn đi thẳng qua một con sông rộng 0,10 km. Động cơ của ca nô tạo cho nó vận tốc 4,0 km/giờ trong nước sông không chảy. Tuy nhiên, có một dòng chảy mạnh đang di chuyển về phía hạ lưu với vận tốc 3,0 km/giờ. Ca nô phải đi theo hướng nào để đến vị trí ở bờ bên kia đối diện với vị trí xuất phát.
Một ca nô muốn đi thẳng qua một con sông rộng 0,10 km. Động cơ của ca nô tạo cho nó vận tốc 4,0 km/giờ trong nước sông không chảy. Tuy nhiên, có một dòng chảy mạnh đang di chuyển về phía hạ lưu với vận tốc 3,0 km/giờ. Ca nô phải đi theo hướng nào để đến vị trí ở bờ bên kia đối diện với vị trí xuất phát.
D. 5 km/h theo hướng về phía hạ lưu.
Quảng cáo
Trả lời:
Đáp án đúng là A
Do nước chảy về phía hạ lưu nên ta có biểu đồ sau.
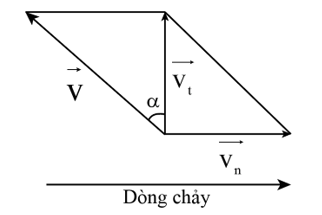
Vận tốc \[v = \sqrt {v_n^2 + v_t^2} = \sqrt {{3^2} + {4^2}} = 5\,km/h\] theo hướng về phía thượng lưu một góc thỏa mãn \[\tan \alpha = \frac{{{v_n}}}{{{v_t}}} = \frac{3}{4} \Rightarrow \alpha = 36,{9^0}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo giả thiết, ta có: \(P\left( 0 \right) = - 25\).
\(P\left( {90} \right) = P\left( 0 \right) + \int\limits_0^{90} {P'\left( x \right)\,} {\rm{d}}x = - 25 + \int\limits_0^{90} {\left( {16 - 0,02x} \right)} \,{\rm{d}}x = - 25 + \left. {\left( {16x - 0,01{x^2}} \right)} \right|_0^{90} = 1\,334\).
Vậy nếu trong tuần nhà máy bán được 90 tấn sản phẩm thì thu được lợi nhuận là 1 334 triệu đồng.
Đáp án cần nhập là: \(1\,334\).Câu 2
Lời giải
Chọn hệ trục tọa độ như hình vẽ dưới.
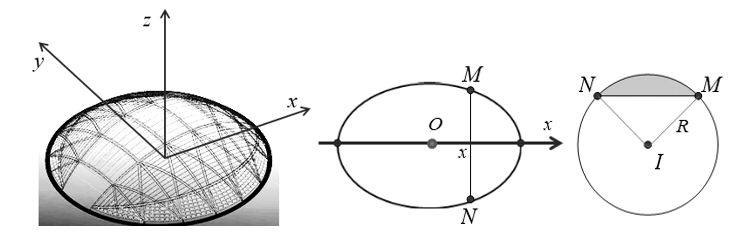
Ta cần tìm diện tích của \(S\left( x \right)\) thiết diện. Gọi \(d\left( {O,MN} \right) = x\).
Ta có \(\left( E \right):\frac{{{x^2}}}{{{{75}^2}}} + \frac{{{y^2}}}{{{{45}^2}}} = 1.\) Lúc đó \[MN = 2y = 2\sqrt {{{45}^2}\left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)} = 90\sqrt {1 - \frac{{{x^2}}}{{{{75}^2}}}} \]
\[ \Rightarrow R = \frac{{MN}}{{\sqrt 2 }} = \frac{{90}}{{\sqrt 2 }} \cdot \sqrt {1 - \frac{{{x^2}}}{{{{75}^2}}}} \Rightarrow {R^2} = \frac{{{{90}^2}}}{2} \cdot \left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)\].
Khi đó, \[S\left( x \right) = \frac{1}{4}\pi {R^2} - \frac{1}{2}{R^2} = \left( {\frac{1}{4}\pi - \frac{1}{2}} \right){R^2} = \left( {\pi - 2} \right)\frac{{2025}}{2} \cdot \left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right).\]
Thể tích khoảng không cần tìm là: \(V = \int\limits_{ - 75}^{75} {\left( {\pi - 2} \right)\frac{{2025}}{2} \cdot \left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)dx \approx 115\,\,586\,\,\left( {{m^3}} \right).} \) Chọn B.
Câu 3
A. As we will eat or drink sugary foods.
B. Eating and drinking sugary foods
C. After we ate or drank sugary foods.
D. When we eat or drink sugary foods.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{{x - 4}}{4} = \frac{{y - 3}}{3} = \frac{{z - 3}}{{ - 7}}\).
B. \(\frac{{x + 4}}{4} = \frac{{y + 3}}{3} = \frac{{z - 3}}{1}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.