Cho hai đường thẳng \(ab\) và \(cd\) cắt nhau tại \(O\) sao cho \(\widehat {aOc} = 120^\circ \). Khẳng định nào dưới đây là đúng?
Quảng cáo
Trả lời:
Đáp án đúng là: C
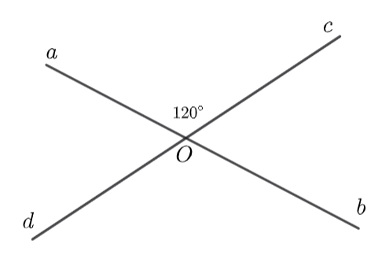
Ta có: \(\widehat {aOc} = \widehat {bOd} = 120^\circ \) (đối đỉnh)
Vì \(\widehat {aOc}\) và \(\widehat {bOc}\) là hai góc kề bù nên \(\widehat {aOc} + \widehat {bOc} = 180^\circ \) hay \(\widehat {bOc} = 180^\circ - \widehat {aOc} = 180^\circ - 120^\circ = 60^\circ \).
Lại có \(\widehat {bOc} = \widehat {aOd} = 60^\circ \) (đối đỉnh).
Do đó, chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
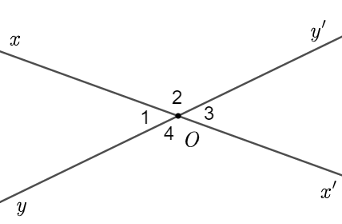
A. \({\widehat O_1}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_3}\).
B. \({\widehat O_1}\) và \({\widehat O_2}\); \({\widehat O_3}\) và \({\widehat O_4}\).
Lời giải
Đáp án đúng là: D
Quan sát hình vẽ, nhận thấy các cặp góc đối đỉnh trong hình trên là \({\widehat O_1}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_4}\).
Lời giải
Đáp án: 80
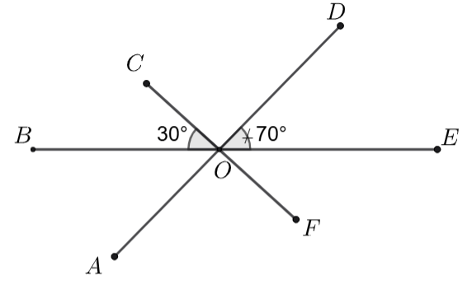
Nhận thấy \(\widehat {EOF} = \widehat {BOC} = 30^\circ \) (hai góc đối đỉnh).
Có \(\widehat {DOE},\,\,\widehat {FOE}\) là hai góc kề nhau nên \(\widehat {DOE} + \,\widehat {FOE} = \widehat {DOF}\) hay \(\widehat {DOF} = 30^\circ + 70^\circ = 100^\circ \).
Lại có \(\widehat {DOF},\,\,\widehat {AOF}\) là hai góc kề bù nên \(\widehat {DOF} + \widehat {AOF} = 180^\circ \).
Suy ra \(\widehat {AOF} = 180^\circ - \widehat {DOF} = 180^\circ - 100^\circ = 80^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
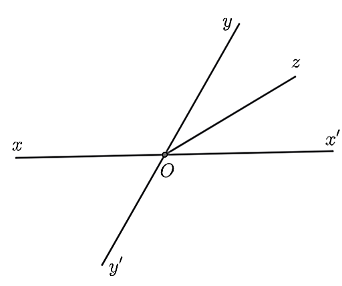
a) \(\widehat {yOz} = 30^\circ .\)
b) \(\widehat {xOy} = 130^\circ .\)
c) \(\widehat {x'Oy} = 60^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.