Lớp 6A có 45 học sinh, trong đó có \[\frac{1}{5}\] số học sinh giỏi, học sinh khá chiếm \[\frac{1}{3}\] số còn lại, còn lại là học sinh trung bình và yếu. Tính số học sinh trung bình và yếu.

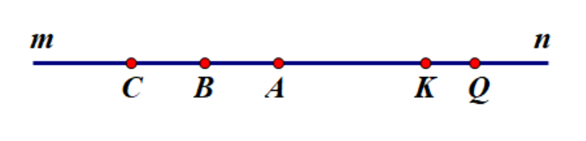
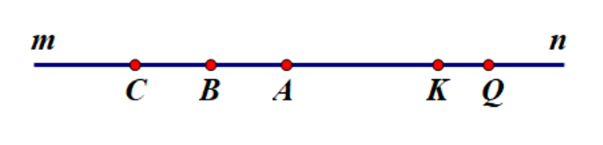
a) Theo đề bài ta có hai điểm \[K\] và \[Q\] đều thuộc tia \[An\].

Mà \(AK < AQ\)A (3 cm < 4 cm) nên điểm \[K\] nằm giữa hai điểm \[A\] và \[Q\].

Do đó ta có: \[AQ = AK + KQ\].

Suy ra \[KQ = AQ--AK = 4--3 = 1\] (cm).

Vậy \[KQ = 1\] cm.

b) Vì điểm \[C\] nằm trên tia \[Am\] là tia đối của \[An\] và \[K \in An\] nên điểm \[A\] nằm giữa hai điểm \[C\] và \[K\].

Suy ra \[CK = AC + AK = 3 + 3 = 6\] (cm);

Vì điểm \[A\] nằm giữa hai điểm \[C\] và \[K\] và \(AC = AK = \frac{1}{2}CK\).

Vậy \[A\] là trung điểm của đoạn thẳng \[CK\]. 

c) Vì \[B\] là trung điểm của đoạn thẳng \[CA = 3\] cm.

Do đó \[BA = \frac{1}{2}CA = \frac{3}{2} = \frac{{15}}{{10}} = 1,5\] (cm).

Mặt khác, \[B \in Am;\,\,K \in An\], với \[Am,{\rm{ }}An\] là hai tia đối nhau nên điểm \[A\] nằm giữa hai điểm \[B\] và \[K\].

Độ dài đoạn thẳng \[BK = BA + AK = 1,5 + 3 = 4,5\] (cm).

Do đó \[BK > AQ\] (4,5 cm  > 4 cm).