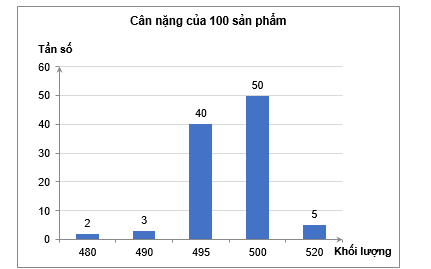
Một nhà máy kiểm tra cân nặng 100 sản phẩm của một dây chuyền đóng gói bánh đang trong thời gian thử nghiệm. Cân nặng của mỗi gói bánh có tiêu chuẩn là 500 gam. Những gói bánh có khối lượng chênh lệch không quá 10 gam so với tiêu chuẩn được xem là đạt yêu cầu. Kết quả kiểm tra được biểu diễn ở biểu đồ dưới đây:
 Trong 100 sản phẩm được kiểm tra, số gói bánh đạt yêu cầu chênh lệch bao nhiêu với số gói bánh không đạt yêu cầu?
Trong 100 sản phẩm được kiểm tra, số gói bánh đạt yêu cầu chênh lệch bao nhiêu với số gói bánh không đạt yêu cầu?

Quảng cáo
Trả lời:
Chọn C
Quan sát biểu đồ, ta thấy:
⦁ Có 2 gói bánh có khối lượng 480 gam.
⦁ Có 3 gói bánh có khối lượng 490 gam.
⦁ Có 40 gói bánh có khối lượng 495 gam.
⦁ Có 50 gói bánh có khối lượng 500 gam.
⦁ Có 5 gói bánh có khối lượng 520 gam.
Ta có:
⦁ Cân nặng của mỗi gói bánh có tiêu chuẩn là 500 gam.
⦁ Những gói bánh có khối lượng chênh lệch không quá 10 gam so với tiêu chuẩn được xem là đạt yêu cầu.
Suy ra các gói bánh đạt yêu cầu là các gói bánh có khối lượng 490 gam; 495 gam; 500 gam.
Do đó có tổng cộng \[3 + 40 + 50 = 93\] gói bánh có khối lượng đạt yêu cầu.
Vì vậy có tổng cộng \[100 - 93 = 7\] gói bánh có khối lượng không đạt yêu cầu.
Vậy số gói bánh đạt yêu cầu chênh lệch \[93 - 7 = 86\] gói bánh so với số gói bánh không đạt yêu cầu, ta chọn phương án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
Bảng kết quả có thể xảy ra:
|
Hộp 1 Hộp 2 |
1 |
2 |
3 |
4 |
5 |
|
6 |
16 |
26 |
36 |
46 |
56 |
|
7 |
17 |
27 |
37 |
47 |
57 |
|
8 |
18 |
28 |
38 |
48 |
58 |
|
9 |
19 |
29 |
39 |
49 |
59 |
Không gian mẫu của phép thử là \(\Omega = \left\{ {16;\,\,26;\,\,36;...;\,\,49;\,\,59} \right\}\).
Do đó, không gian mẫu của phép thử có 20 phần tử.
Câu 2
Lời giải
Chọn B
- Ta viết các tập hợp con có hai phần tử của tập hợp \(\left\{ {1;2;3;4} \right\}\).
\[\Omega = \left\{ {\left( {1;2} \right);\left( {1;3} \right);\left( {1;4} \right);\left( {2;3} \right);\left( {2;4} \right);\left( {3;4} \right)} \right\} \Rightarrow {\rm{n}}\left( \Omega \right) = 6.{\rm{ }}\]
Xét biến cố \(E\): “Tích hai số ghi trên hai viên bi lớn hơn 3”.
Ta có: \[E = \left\{ {\left( {1;4} \right);\left( {2;3} \right);\left( {2;4} \right);\left( {3;4} \right)} \right\} \Rightarrow n\left( E \right) = 4\]. Vậy \(P\left( E \right) = \frac{2}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.