Cho hai biểu thức:
\(A = \frac{2}{{5.7}} + \frac{5}{{7\,.\,\,12}} + \frac{7}{{12\,.\,19}} + \frac{9}{{19\,.\,28}} + \frac{{11}}{{28\,.\,39}} + \frac{1}{{39\,.\,40}}\) và \[B = \frac{1}{{20}} + \frac{1}{{44}} + \frac{1}{{77}} + \frac{1}{{119}} + \frac{1}{{170}}.\]
Chứng minh \(A > B\).
Cho hai biểu thức:
\(A = \frac{2}{{5.7}} + \frac{5}{{7\,.\,\,12}} + \frac{7}{{12\,.\,19}} + \frac{9}{{19\,.\,28}} + \frac{{11}}{{28\,.\,39}} + \frac{1}{{39\,.\,40}}\) và \[B = \frac{1}{{20}} + \frac{1}{{44}} + \frac{1}{{77}} + \frac{1}{{119}} + \frac{1}{{170}}.\]
Chứng minh \(A > B\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Ta có: \(A = \frac{2}{{5.7}} + \frac{5}{{7.12}} + \frac{7}{{12.19}} + \frac{9}{{19.28}} + \frac{{11}}{{28.39}} + \frac{1}{{39.40}}\)
\( = \frac{1}{5} - \frac{1}{7} + \frac{1}{7} - \frac{1}{{12}} + \frac{1}{{12}} - \frac{1}{{19}} + \frac{1}{{19}} - \frac{1}{{28}} + \frac{1}{{28}} - \frac{1}{{39}} + \frac{1}{{39}} - \frac{1}{{40}}\)
\( = \frac{1}{5} - \frac{1}{{40}}\)\( = \frac{8}{{40}} - \frac{1}{{40}} = \frac{7}{{40}}\);
\[B = \frac{1}{{20}} + \frac{1}{{44}} + \frac{1}{{77}} + \frac{1}{{119}} + \frac{1}{{170}}\]
\[ = \frac{2}{{40}} + \frac{2}{{88}} + \frac{2}{{154}} + \frac{2}{{238}} + \frac{2}{{340}}\]
\[ = 2.\left( {\frac{1}{{5.8}} + \frac{1}{{8.11}} + \frac{1}{{11.14}} + \frac{1}{{14.17}} + \frac{1}{{17.20}}} \right)\]
\[ = 2.\frac{1}{3}.\left( {\frac{3}{{5.8}} + \frac{3}{{8.11}} + \frac{3}{{11.14}} + \frac{3}{{14.17}} + \frac{3}{{17.20}}} \right)\]
\[ = \frac{2}{3}.\left( {\frac{1}{5} - \frac{1}{8} + \frac{1}{8} - \frac{1}{{11}} + \frac{1}{{11}} - \frac{1}{{14}} + \frac{1}{{14}} - \frac{1}{{17}} + \frac{1}{{17}} - \frac{1}{{20}}} \right)\]
\[ = \frac{2}{3}.\left( {\frac{1}{5} - \frac{1}{{20}}} \right)\]\[ = \frac{2}{3}.\left( {\frac{4}{{20}} - \frac{1}{{20}}} \right)\]\[ = \frac{2}{3}.\frac{3}{{20}}\]\[ = \frac{1}{{10}}\].
Ta có: \(\frac{7}{{40}} > \frac{4}{{40}} = \frac{1}{{10}}\). Do đó \(A > B\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1.
a) \(11\frac{3}{{13}} - \left( {2\frac{4}{7} + 5\frac{3}{{13}}} \right) = \left( {11 + \frac{3}{{13}}} \right) - \left[ {\left( {2 + \frac{4}{7}} \right) + \left( {5 + \frac{3}{{13}}} \right)} \right]\)
\( = 11 + \frac{3}{{13}} - \left[ {7 + \frac{4}{7} + \frac{3}{{13}}} \right] = 11 + \frac{3}{{13}} - 7 - \frac{4}{7} - \frac{3}{{13}} = 4 - \frac{4}{7} = \frac{{24}}{7}\);
b) \[\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7} = \frac{{ - 5}}{7}\left( {\frac{2}{{11}} + \frac{9}{{11}}} \right) + \frac{5}{7} = \frac{{ - 5}}{7} \cdot 1 + \frac{5}{7} = 0\].
2.
|
a) \[\frac{3}{7} + x = \frac{4}{5}\] \[x = \frac{4}{5} - \frac{3}{7}\] \[x = \frac{{28}}{{35}} - \frac{{15}}{{35}}\] \[x = \frac{{13}}{{35}}\] Vậy \[x = \frac{{13}}{{35}}\]. |
b) \[\left( {3x - 1} \right)\left( {\frac{{ - 1}}{2}x + 5} \right) = 0\] • TH1: \[3x--1 = 0\] \[3x = 1\] \[x = \frac{1}{3}\]. • TH2: \[\frac{{ - 1}}{2}x + 5 = 0\] \[\frac{{ - 1}}{2}x = - 5\] \[x = - 5:\left( {\frac{{ - 1}}{2}} \right)\] \[x = 10\]. Vậy \[x \in \left\{ {\frac{1}{3};\,\,10} \right\}\]. |
Lời giải
Số tiền được giảm giá của món đồ chơi là:
\[50\,\,000\,\,.\,\,10\% = 5{\rm{ }}000\] (đồng);
Số tiền Nam phải trả để mua món đồ chơi đó là:
\[50{\rm{ }}000--5{\rm{ }}000 = 45{\rm{ }}000\] (đồng)
Vậy Nam phải trả \[45{\rm{ }}000\] đồng để mua món đồ chơi đó.
Lời giải
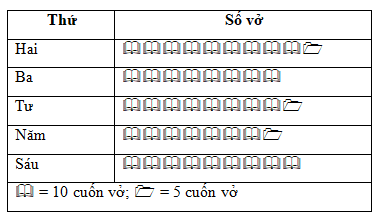
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.