Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
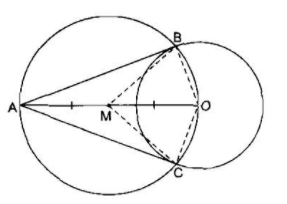
Ta có: MA = MO = MB ( cùng bằng bán kính đường tròn tâm M, bán kính MO)
MA = MB ⇒ ΔMAB cân tại M ⇒ ∠(BAO) = ∠(ABM)
MO=MB⇒ΔMOB cân tại M ⇒∠(BOA) = ∠(MBO)
⇒∠(BAO) + ∠(BOA) = ∠(ABM) + ∠(MBO) = ∠(ABO) (1)
Mặt khác ta lại có: ∠(BAO) + ∠(BOA) + ∠(ABO) = 180o (2) (tổng 3 góc trong tam giác)
Từ (1) và (2) ⇒ ∠(ABO) = 90o
Hay AB là tiếp tuyến của (O)
Chứng minh tương tự, ta được AC là tiếp tuyến của (O)
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
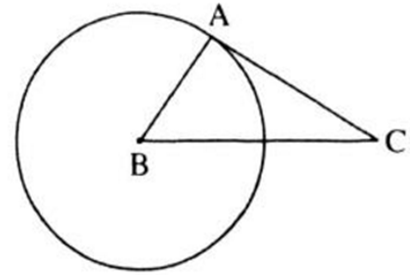
Ta có: AB2 + AC2 = 32 + 42 = 25
BC2 = 52 = 25
Nên AB2 + AC2 = BC2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.
Lời giải
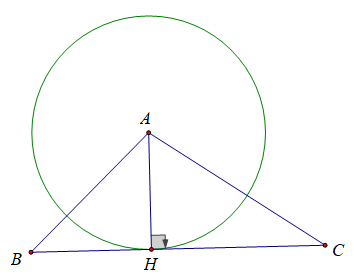
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo