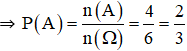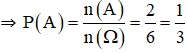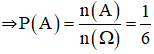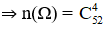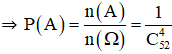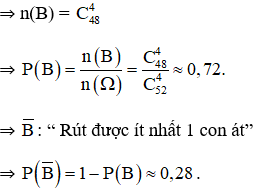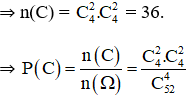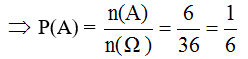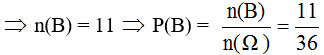Câu hỏi:
12/07/2024 19,763Gieo một con súc sắc cân đối và đồng nhất. giả sử con súc sắc xuất hiện mặt b chấm. Xét phương trình . Tính xác suất sao cho:
a. Phương trình có nghiệm
b. Phương trình vô nghiệm
c. Phương tring có nghiệm nguyên.
Câu hỏi trong đề: Giải toán 11: Đại số và Giải tích !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Không gian mẫu khi gieo con súc sắc cân đối và đồng chất:
Ω = {1, 2, 3, 4, 5, 6}
⇒ n(Ω) = 6
Đặt A: "con súc sắc xuất hiện mặt b chấm";
Xét : x2 + bx + 2 = 0 (1)
Δ = b2 – 8
a. Phương trình (1) có nghiệm
⇔ Δ ≥ 0 ⇔ b ≥ 2√2
⇒ b ∈ {3; 4; 5; 6}.
⇒ A = {3, 4, 5, 6}
⇒ n(A) = 4
b. (1) vô nghiệm
⇔ Δ < 0 ⇔ b ≤ 2√2
⇒ b ∈ {1; 2}
⇒ A = {1, 2}
⇒ n(A) = 2
c. phương trình (1) có nghiệm
⇔ b ∈ {3; 4; 5; 6}.
Thử các giá trị của b ta thấy chỉ có b = 3 phương trình cho nghiệm nguyên.
⇒ A = {3}
⇒ n(A) = 1
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 4 con trong số 52 con
a. Đặt A : « Cả 4 con lấy ra đều là át »
⇒ n(A) = 1
b. + B : « Không có con át nào trong 4 con khi lấy ra »
⇒ B là kết quả của việc chọn ngẫu nhiên 4 con trong số 48 con còn lại
c. C: “Rút được 2 con át và 2 con K”.
Lời giải
a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 6
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án