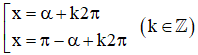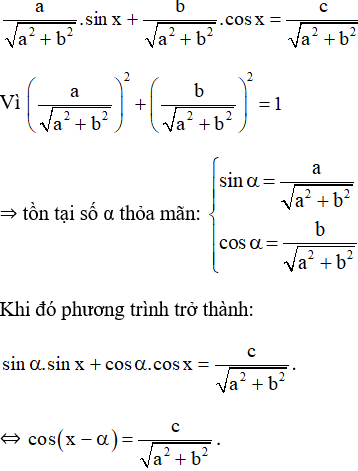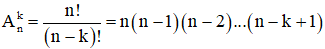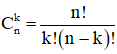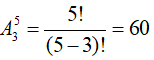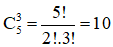Câu hỏi:

13/07/2024 1,255

Nêu rõ các bước chứng minh bằng quy nạp toán học và cho ví dụ

Xem lời giải

Câu hỏi trong đề: Giải toán 11: Đại số và Giải tích !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

+ Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈ N* là đúng với mọi n mà không thể thử trực tiếp được thì ta làm như sau:

Bước 1: Kiểm tra mệnh đề đúng với n = 1 .

Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1. Chứng minh rằng nó cũng đúng với n = k+1.

Bước 3: Kết luận mệnh đề đúng với n ∈ N*.

+ Ví dụ: Chứng minh rằng với mọi n ∈ N* ta có: n3 + 5n chia hết cho 6.

Chứng minh: Đặt P(n) = n3 + 5n.

Với n =1 ⇒ P(1) = 6 ⋮ 6

Giả sử (Pn) chia hết cho 6 đúng với n=k ≥1, nghĩa là, ta có:

P(k) = (k3 + 5k) ⋮ 6.

Ta có: P(k+1) = (k+1)3 + 5(k+1) = k3 + 3k2 + 3k + 1 + 5k + 5 = k3 + 5k + 3(k2 + k) + 6

Mặt khác, theo giả thiết quy nạp ta có: k3 + 5k ⋮6.

Hơn nữa k2 + k = k(k+1) : 2 ( hai số tự nhiên tiếp k, k +1 phải có một số chẵn do k(k+1):2).

Do vậy P(k+1)⋮6. Tức mệnh đề đúng với n = k + 1.

Theo nguyên lí quy nạp, ta có P(n) = n3 + 5n chia hết cho 6 với mọi n ∈ N*.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Nêu cách giải phương trình lượng giác cơ bản , cách giải phương trình $a \sin x + b \cos x = c$ .

Xem đáp án

Lời giải

a) Cách giải các phương trình lượng giác cơ bản:

+ Phương trình sin x = a.

Nếu |a| > 1 ⇒ phương trình vô nghiệm.

Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.

Khi đó phương trình trở thành sin x = sin α

⇒ Phương trình có nghiệm: Giải bài 3 trang 178 sgk Đại số 11 | Để học tốt Toán 11

+ Phương trình cos x = a.

Nếu |a| > 1 ⇒ phương trình vô nghiệm.

Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.

Khi đó phương trình trở thành cos x = cos α.

⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).

+ Phương trình tan x = a.

Tìm một cung α sao cho tan α = a.

Khi đó phương trình trở thành tan x = tan α.

⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).

+ Phương trình cot x = a

Tìm một cung α sao cho cot α = a.

Khi đó phương trình trở thành cot x = cot α.

⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).

b) Cách giải phương trình a.sin x + b.cos x = c.

+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .

+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho 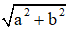Giải bài 3 trang 178 sgk Đại số 11 | Để học tốt Toán 11 ta được:

Giải bài 3 trang 178 sgk Đại số 11 | Để học tốt Toán 11

Ta giải phương trình trên như phương trình lượng giác cơ bản.

Câu 2

Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.

Xem đáp án

Lời giải

+ Số chỉnh hợp chập k của n phần tử:

Giải bài 5 trang 178 sgk Đại số 11 | Để học tốt Toán 11

+ Số tổ hợp chập k của n phần tử:

Giải bài 5 trang 178 sgk Đại số 11 | Để học tốt Toán 11

+ Ví dụ:

- Số chỉnh hợp chập 3 của 5: Giải bài tập Toán 11 | Giải Toán lớp 11

- Số tổ hợp chập 3 của 5: Giải bài 5 trang 178 sgk Đại số 11 | Để học tốt Toán 11

- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:

⇒ Có 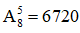Giải bài 5 trang 178 sgk Đại số 11 | Để học tốt Toán 11 cách chọn.

- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau

⇒ Có 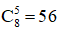Giải bài 5 trang 178 sgk Đại số 11 | Để học tốt Toán 11 cách chọn.

Câu 3