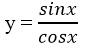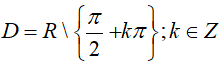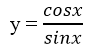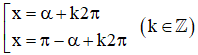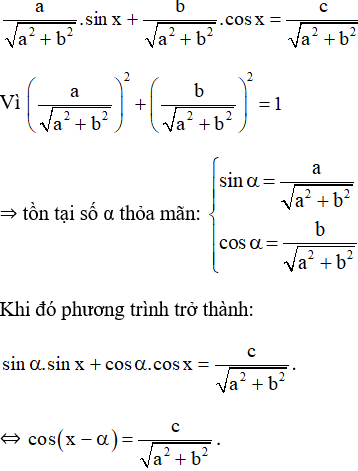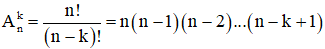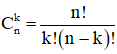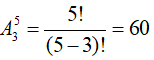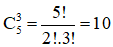Câu hỏi Ôn tập cuối năm
22 người thi tuần này 5.0 61.4 K lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a. Định nghĩa 1 : (Hàm số sin): Quy tắc tương ứng với mỗi số thực x với số thực sinx.
sin: R -> R
x -> y = sinx.
Hàm số y = sinx có tập xác định là R, tập giá trị là đoạn [-1;1].
b.Định nghĩa 2 : (Hàm số cosin): Quy tắc tương ứng với mỗi số thực x với số thực cosx.
cos : R -> R
x -> y = cosx.
Hàm số y = cosx có tập xác định là R, tập giá trị là đoạn [-1;1]
c. Định nghĩa 3: (Hàm số tang): Hàm số tang là hàm số được xác định bởi công thức
tan : D -> R
x -> y = tanx.
Hàm số y = tanx có tập xác định:
Tập giá trị của hàm số y = tanx là R.
d. Định nghĩa 4 : (Hàm số cotang): là hàm số được xác định bởi công thức
cot : D -> R
x -> y = cotx.
Hàm số y = cotx có tập xác định D = {x ∈ R \ x ≠ kπ, k ∈ Z}. Tập giá trị của hàm số y = cotx là tập R.
Lời giải
a. Hàm số y = sinx và y = cosx là hàm số tuần hoàn có chu kì là 2 π.
b. Hàm số y = tanx và y = cotx là các hàm số tuần hoàn có chu kì là π.
Lời giải
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm:
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho 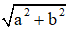
Ta giải phương trình trên như phương trình lượng giác cơ bản.
Lời giải
+ Cho tập A gồm n phần tử.
Mỗi hoán vị của A là kết quả của sự sắp xếp thứ tự n phần tử của tập A.
+ Số các hoán vị: Pn = n! = 1.2.3.4.5….n.
Ví dụ: Số hoán vị của tập gồm 6 phần tử là: P6 = 6! = 720.
Số hoán vị của tập gồm 3 phần tử là: P3 = 6.
Lời giải
+ Số chỉnh hợp chập k của n phần tử:
+ Số tổ hợp chập k của n phần tử:
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5:
- Số tổ hợp chập 3 của 5:
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có 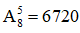
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có 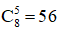
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.