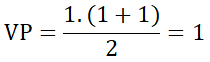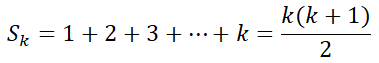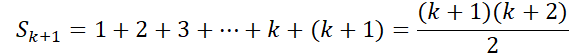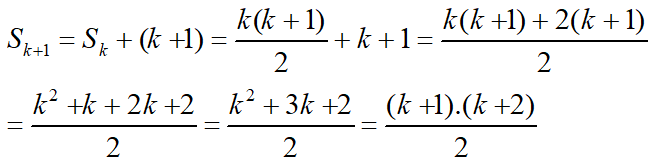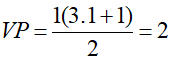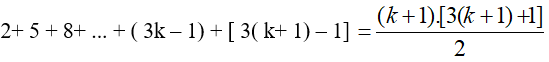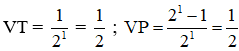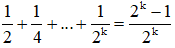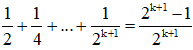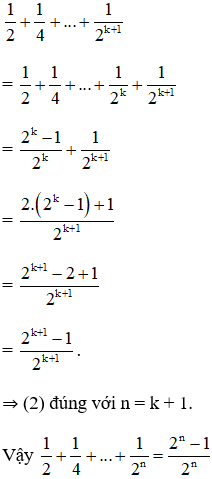Bài 1: Phương pháp quy nạp toán học
16 người thi tuần này 5.0 61.4 K lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) Xét P(n) : “3n < n + 100”:
+ Với n = 1, P(1) trở thành: “31 < 1 + 100”. Mệnh đề đúng vì 31 = 3 < 1 + 100 = 101.
+ Với n = 2, P(2) trở thành: “32 < 2 + 100”. Mệnh đề đúng vì 32 = 9 < 2 + 100.
+ Với n = 3, P(3) trở thành: “33 < 3 + 100”. Mệnh đề đúng vì 33 = 27 < 3 + 100.
+ Với n = 4, P(4) trở thành: “34 < 4 + 100”. Mệnh đề đúng vì 34 = 81 < 4 + 100.
+ Với n = 5, P(5) trở thành: “35 < 5 + 100”. Mệnh đề sai vì 35 = 243 > 5 + 100.
Xét Q(n): “2n > n”.
+ Với n = 1, Q(1) trở thành: “21 > 1”. Mệnh đề đúng vì 21 = 2 > 1.
+ Với n = 2, Q(2) trở thành: “22 > 2”. Mệnh đề đúng vì 22 = 4 > 2.
+ Với n = 3, Q(3) trở thành: “23 > 3”. Mệnh đề đúng vì 23 = 8 > 3.
+ Với n = 4, Q(4) trở thành: “24 > 4”. Mệnh đề đúng vì 24 = 16 > 4.
+ Với n = 5, Q(5) trở thành: “25 > 5”. Mệnh đề đúng vì 25 = 32 > 5.
b)
+ Nhận thấy P(n) không đúng với mọi n ∈ N* (sai với n = 5).
+ Với mọi n ∈ N*, Q(n) luôn đúng.
Lời giải
- Khi n = 1, VT = 1;
⇒ VT = VP , do đó đẳng thức đúng với n = 1.
- Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là:
Ta phải chứng minh rằng đẳng thức cũng đúng với n = k + 1, tức là:
Thật vậy, từ giả thiết quy nạp ta có:
Vậy đẳng thức đúng với mọi n ∈ N*
Lời giải
a)n = 1 ⇒ 31 = 3 < 8 = 8.1
n = 2 ⇒ 32 = 9 < 16 = 8.2
n = 3 ⇒ 33 = 27 > 24 = 8.3
n = 4 ⇒ 34 = 81 > 32 = 8.4
n = 5 ⇒ 35 = 243 > 40 = 8.5
b) Dự đoán kết quả tổng quát: 3n > 8n với mọi n ≥ 3
- n = 3, bất đẳng thức đúng
- Giả sử bất đẳng thức đúng với n = k ≥ 3, nghĩa là:
3k > 8k
Ta phải chứng minh rằng bất đẳng thức cũng đúng với n = k + 1, tức là:
3(k + 1) > 8(k + 1)
Thật vậy, từ giả thiết quy nạp ta có:
3(k + 1) = 3k.3 > 8k.3 = 24k = 8k + 16k
k ≥ 3 ⇒ 16k ≥ 16.3 = 48 > 8
Suy ra: 3(k + 1) > 8k + 8 = 8(k + 1)
Vậy bất đẳng thức đúng với mọi n ≥ 3
Lời giải
+ Với n = 1, ta có:
VT = 3 – 1 = 2
⇒ VT = VP
⇒ (1) đúng với n = 1
+ Giả sử (1) đúng với n = k ≥ 1 nghĩa là:
2 + 5 + 8 + …+ (3k – 1) = k(3k + 1)/2. (*)
Ta cần chứng minh (1) đúng với n = k + 1, tức là :
Thật vậy :
Ta có :
Lời giải
+ Với n = 1 :
Vậy (2) đúng với n = 1
+ Giả sử đẳng thức đúng với n = k, tức là:
Cần chứng minh (2) đúng với n = k + 1, tức là:
Thật vậy, ta có :
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.