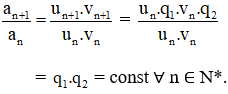Ôn tập chương 3
21 người thi tuần này 5.0 61.4 K lượt thi 19 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Cấp số cộng (un) có công sai d.
+ (un) là dãy tăng
⇔ un + 1 > un ∀ n ∈ N
⇔ un + 1 – un > 0 ∀ n ∈ N
⇔ d > 0
+ (un) là dãy giảm
⇔ un + 1 < un ∀ n ∈ N
⇔ un + 1 – un < 0 ∀ n ∈ N
⇔ d < 0
Lời giải
CSN (un) : un = u1.qn – 1, u1 < 0
a. q > 0 ⇒ qn – 1 > 0 ⇒ u1.qn – 1 < 0 (vì u1 < 0)
⇒ un < 0 với mọi n ∈ N*.
Vậy với q > 0 và u1 < 0 thì các số hạng đều mang dấu âm.
b. q < 0.
+ Nếu n chẵn ⇒ n – 1 lẻ ⇒ qn – 1 < 0
⇒ u1.qn – 1 > 0 (vì u1 < 0).
⇒ un > 0.
+ Nếu n lẻ ⇒ n – 1 chẵn ⇒ qn – 1 > 0
⇒ u1.qn – 1 < 0 (Vì u1 < 0).
⇒ un < 0.
Vậy nếu q < 0, u1 < 0 thì các số hạng thứ chẵn dương và các số hạng thứ lẻ âm.
Lời giải
Giả sử có hai cấp số cộng (un) với công sai d1 và (vn) với công sai d2.
Xét dãy (an) với an = un + vn
Ta có: an + 1 – an = (un + 1 + vn + 1) – (un + vn)
= (un + d1 + vn + d2) – (un + vn)
= d1 + d2 = const
⇒(an) là cấp số cộng với công sai d1 + d2.
Ví dụ:
CSC (un): 1; 4; 7; 10; 13; 16; 19; …. có công sai d1 = 3 ;
CSC (vn): 4 ; 6 ; 8 ; 10 ; 12 ; 14 ; 16 … có công sai d2 = 2.
⇒ (an): 5; 10; 15; 20; 25; 30; 35; … có công sai d = 5.
Lời giải
Giả sử có hai cấp số nhân (un) với công bội q1 và (vn) với công bội q2.
Xét dãy số (an) với an = un.vn với mọi n ∈ N*.
Ta có:
⇒ (an) là cấp số nhân với công bội q1.q2.
Ví dụ:
+ CSN (un) : 2 ; 4 ; 8 ; 16 ; 32 ; 64 ; … có công bội q1 = 2.
+ CSN (vn) : -1 ; 1 ; -1 ; 1 ; -1 ; 1 ; … có công bội q2 = -1.
⇒ CSN (an) : -2 ; 4 ; -8 ; 16 ; -32 ; 64 ; … có công bội q = -2.
Lời giải
Đặt un = 13n – 1
+ Với n = 1 thì u1 = 13 – 1 = 12 chia hết 6
+ Giả sử: uk = 13k – 1 chia hết cho 6.
⇒ uk + 1 = 13k + 1 – 1
= 13k+1 + 13k – 13k – 1
= 13k(13 – 1) + 13k – 1
= 12.13k + uk.
Mà 12.13k ⋮ 6; uk ⋮ 6.
⇒ uk + 1 ⋮ 6.
⇒ un ⋮ 6 với mọi n ∈ N.
hay 13n – 1 ⋮ 6 với mọi n ∈ N.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.