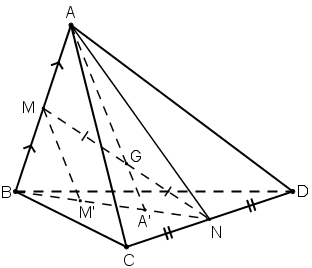
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
Câu hỏi trong đề: Giải toán 11: Hình học !!
Quảng cáo
Trả lời:
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
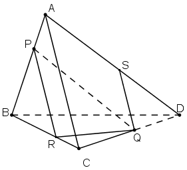
mp(PQR) và mp(ACD) lần lượt chứa hai đường thẳng song song PR // AC
⇒ (PQR) ∩ (ACD) = Qt là đường thẳng song song với AC và PR.
Gọi Qt ∩ AD = S
⇒ S = AD ∩ (PQR).
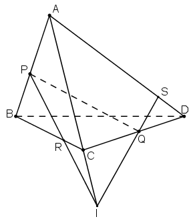
b) PR ∩ AC = I.
Có : Q ∈ (ACD) ∩ (PQR)
+ (ABC) ∩ (PQR) = PR.
+ (ACD) ∩ (ABC) = AC
+ (ACD) cắt (PQR)
⇒ PR; AC và giao tuyến của (ACD) và (PQR) đồng quy
Mà PR ∩ AC = I
⇒ I ∈ (ACD) ∩ (PQR).
⇒ (ACD) ∩ (PQR) = QI.
trong (ACD): QI ∩ AD = S chính là giao tuyến của (PQR) và AD.
Lời giải
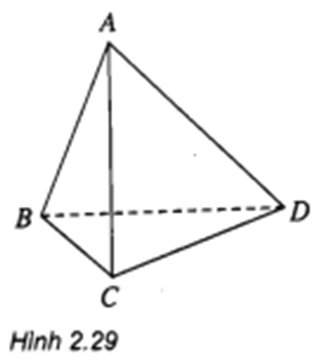
Không tìm được mặt phẳng nào chứa AB và CD ⇒ AB và CD chéo nhau
Các cặp đường thẳng chéo nhau khác của tứ diện này: AC và BD, BC và AD
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.