Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
25 người thi tuần này 5.0 39.6 K lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập Vận dụng đạo hàm cấp hai để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)
Bài tập Vận dụng các quy tắc tính đạo hàm để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)
Bài tập Vận dụng định nghĩa đạo hàm vào giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)
Bài tập Các bài toán thực tiễn vận dụng công thức nhân xác suất lớp 11 (có lời giải)
Bài tập Biến cố độc lập lớp 11 (có lời giải)
Danh sách câu hỏi:
Lời giải
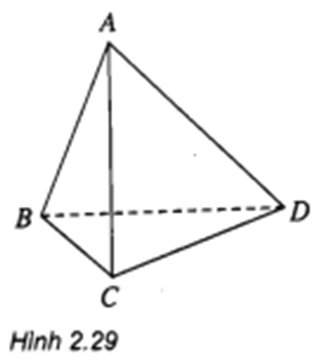
Không tìm được mặt phẳng nào chứa AB và CD ⇒ AB và CD chéo nhau
Các cặp đường thẳng chéo nhau khác của tứ diện này: AC và BD, BC và AD
Lời giải
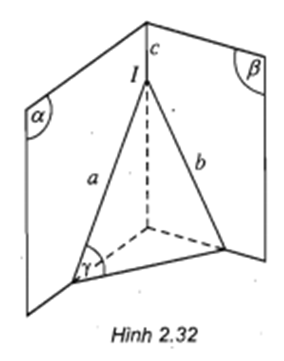
a và b cắt nhau tại I
I ∈ a ∈ α (vì a là giao tuyến của α và λ)
I ∈ b ∈ β ( vì b là giao tuyến của β và λ)
Nên I là điểm chung của α và β
Lời giải
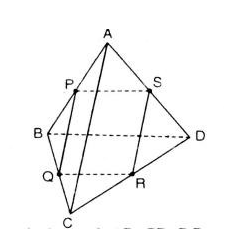
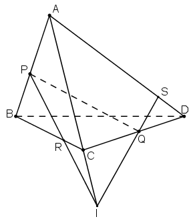
a) Ta có:
PQ = (ABC) ∩ (PQRS)
RS = (PQRS) ∩ (ACD)
AC = (ABC) ∩ (ACD)
Vậy hoặc PQ, RS, AC đồng qui hoặc song song.
b) PS =(ABD) ∩ (PQRS)
RQ = (BCD) ∩ (PQRS)
BD = (ABD) ∩ (CBD)
Vậy PS, RQ, BD đồng quy hoặc song song.
Lời giải
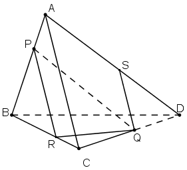
mp(PQR) và mp(ACD) lần lượt chứa hai đường thẳng song song PR // AC
⇒ (PQR) ∩ (ACD) = Qt là đường thẳng song song với AC và PR.
Gọi Qt ∩ AD = S
⇒ S = AD ∩ (PQR).
b) PR ∩ AC = I.
Có : Q ∈ (ACD) ∩ (PQR)
+ (ABC) ∩ (PQR) = PR.
+ (ACD) ∩ (ABC) = AC
+ (ACD) cắt (PQR)
⇒ PR; AC và giao tuyến của (ACD) và (PQR) đồng quy
Mà PR ∩ AC = I
⇒ I ∈ (ACD) ∩ (PQR).
⇒ (ACD) ∩ (PQR) = QI.
trong (ACD): QI ∩ AD = S chính là giao tuyến của (PQR) và AD.
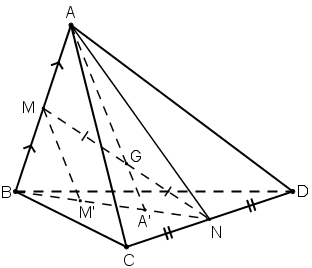
Lời giải
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.
Nhắn tin Zalo
Hỏi bài tập