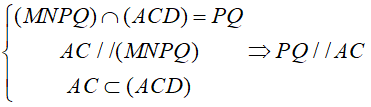Bài 3: Đường thẳng và mặt phẳng song song
41 người thi tuần này 5.0 41.4 K lượt thi 4 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Tạ Quang Bửu (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Nguyễn Bỉnh Khiêm (Hà Nội) có đáp án
Trắc nghiệm Công thức nhân xác suất cho hai biến cố độc lập lớp 11 (có đúng sai, trả lời ngắn)
Trắc nghiệm Công thức cộng xác suất lớp 11 (có đúng sai, trả lời ngắn)
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 0123
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Vì M, N, P lần lượt là trung điểm của AB, AC, AD nên MN, NP, MP lần lượt là đường trung bình của tam giác ABC, ACD, ABD
⇒ MN//BC, NP//CD, PM //BD
Mà BC, CD, BD thuộc (BCD)
MN, NP, PM không thuộc (BCD)
⇒ Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
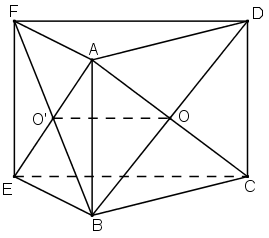
a) Do các tứ giác ABCD và ABEF là các hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO' // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC
mà EC ⊂ (BCE)
⇒ OO’ // (BCE).
b)
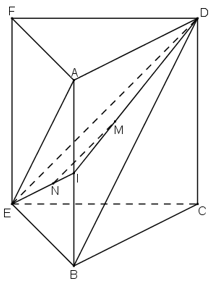
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
⇒ MN // DE mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
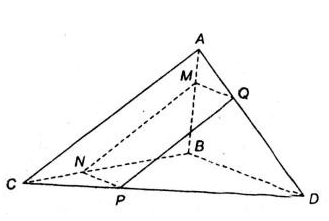
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
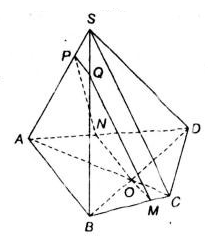
Lời giải
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập