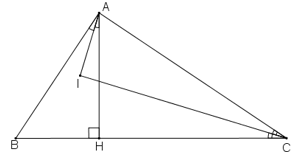
Cho tam giác ABC có ∠A=90o, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. Chứng minh rằng: ∠(AIC)=90o
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 1 !!
Quảng cáo
Trả lời:
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
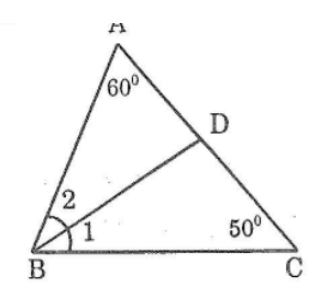
Trong ΔABC ta có:
∠A + ∠B + ∠C = 180o(tổng ba góc trong tam giác)
⇒∠B = 180o - (∠A +∠C )
⇒x = 180o - (60o + 50o) = 70o
(∠B1) =(∠B2 ) = (1/2 )∠B (vì BD là tia phân giác)
⇒ ∠B1 = ∠B2 = 70o : 2 = 35o
Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D
⇒ ∠(ADB) = ∠(B1 ) + ∠C (tính chất góc ngoài tam giác)
Nên ∠(ADB) = 35º + 50º = 85º
+) Do ∠(ADB) + ∠(BDC) = 180o(hai góc kề bù)
⇒∠(BDC) = 180o-∠(ADB) = 180o - 85o = 95o
Lời giải
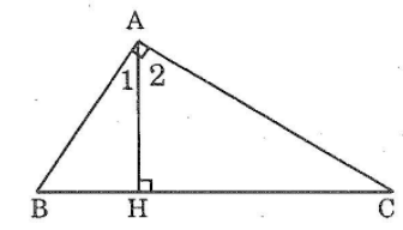
Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.